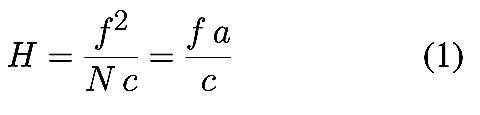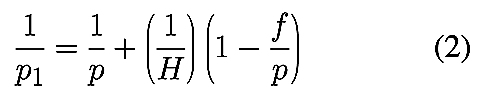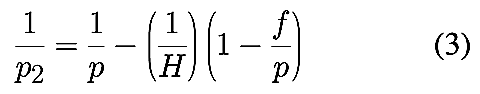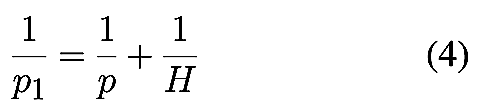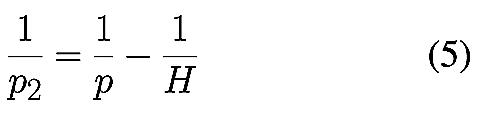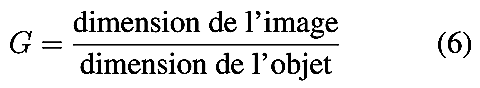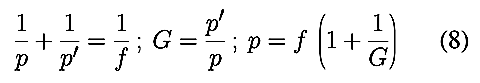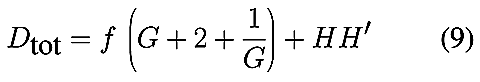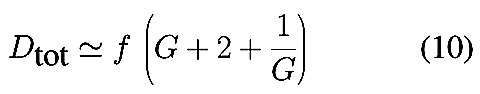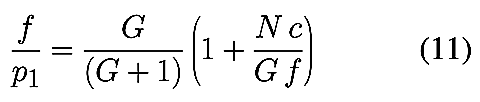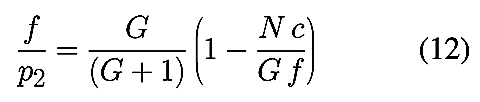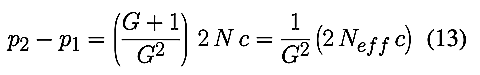[abonnement gratuit]
l'auteur
|
Emmanuel Bigler
est professeur (aujourd'hui retraité) d'optique et des
microtechniques à l'école d'ingénieurs de mécanique et des
microtechniques (ENSMM) de Besançon.
Il a fait sa thèse à l'Institut d'optique à Orsay
E. Bigler utilise par ailleurs une chambre Arca-Swiss
Mail

|
Télécharger l'article
au format pdf
|
|
Décentrements, bascules et règle de Scheimpflug
en petits et moyens formats
Emmanuel BIGLER
ENSMM, 26 chemin de l’Épitaphe, F-25030 Besançon
cedex,
mél :
Mail
Résumé :
Basculer et décentrer l’objectif photographique par rapport au film, c’était
naguère, à de rares exceptions près, la «chasse gardée» des chambres grand
format. La règle de Scheimpflug
n’était connue que des grand-formistes professionnels. Aujourd’hui que les
professionnels n’utilisent plus beaucoup la chambre, on peut se demander s’il y
a toujours un intérêt à appliquer des bascules et des décentrements avec les
appareils de petit et moyen format. Les récents matériels et accessoires
proposés par les constructeurs ainsi que la pratique actuelle de certains
professionnels nous prouvent, au contraire, que bascules et décentrements n’ont
pas encore dit leur dernier mot.
Introduction
Les cours de formation photographique professionnelle classiques [1],
[2], [3], [4], [5],
devaient consacrer une partie importante de leur pagination à la question des
mouvements de la chambre grand format : bascules et décentrements. Il y a donc,
dans la photographie du siècle dernier, deux mondes distincts ; celui des petits
et moyens formats, où sauf rares exceptions, le seul déplacement autorisé à
l’objectif est, pour la mise au point, la translation suivant l’axe optique
(axe orienté de façon intangible, bien perpendiculairement au film, bascule
nulle), l’axe optique pointant toujours vers le centre du format
(décentrement nul). Et puis il y a le monde de la chambre grand format, où,
tout au contraire, toutes les possibilités de bascules et de décentrements sont
non seulement possibles, mais sont absolument requises pour que l’image
satisfasse les critères de la photographie professionnelle d’architecture ou
d’objets en studio.
Certes, même après que l’appareil 24x36 à film ait conquis une position
hégémonique, dans la deuxième moitié du XX siècle, il y avait bien quelques
«oiseaux rares» en petit et moyen format, ces fameuses exceptions qui
confirment la règle, comme les optiques à bascule et décentrement pour
boîtiers reflex 24x36 ; ou bien, en moyen format, la bascule du Rolleiflex SL-66
ou celle du Fuji GX-680, l’adaptateur pour décentrement PC-Mutar du système
Hasselblad-V, le Flex-Body et l’Arc Body du même fabricant, les dispositifs
étranges de la firme Zörkendörfer, ou les optiques moyen format de Kiev
remontées sur bascule & décentrement pour un usage en 24x36.
Aujourd’hui où, nous dit-on, la majorité des professionnels n’utilise
pratiquement plus de film et encore moins de chambres grand format, sauf
peut-être pour leurs activités personnelles ou de loisirs, il serait logique que
bascules et décentrements n’aient plus aucun intérêt, sinon pour quelqu’amateur
désireux de travailler «à l’ancienne» ; mais alors sans contrainte commerciale.
Et les photographes conservateurs, nostalgiques de la vieille école, n’en
finissent plus de se plaindre des prétendues photos d’architecture où les
verticales convergent aujourd’hui abominablement, que ce soit sur les pages web
ou dans les imprimés [6].
Car si les verticales convergent, hop, en un clic de souris en
post-production, on remet, nous dit-on, tout cela d’aplomb en un clin d’œil.
Plus besoin de décentrer, donc. Quant à la règle de Scheimpflug [7],
c’était probablement un vieux truc du temps de Saint Ansel (Adams) [8]
pour pallier le manque de profondeur de champ des longues focales du grand
format : en petit et moyen format, et en numérique, ne dit-on pas souvent qu’on
a trop de profondeur de champ ? Du coup, bascules et tout le «fatras» autour de
Scheimpflug deviendraient, de ce fait, parfaitement inutiles.
Or, situation fort étrange de l’an 2010, voilà qu’une lecture régulière des
annonces des nouveautés des fabricants nous porte à croire qu’il n’en est rien.
Hasselblad met au catalogue un dispositif qui ressemble fort au PC-Mutar, pour
son système H, avec une bascule couplée au calculateur interne à l’appareil ;
Canon et Nikon remettent à jour leurs optiques à bascule et décentrement pour
leurs boîtiers reflex 24x36, Carl Zeiss coopère (depuis quelques temps déjà)
avec Hartblei pour offrir une monture basculante à ses optiques couvrant le 6x6,
et à la Photokina 2010, Schneider-Kreuznach présente trois nouveaux objectifs à
bascule et décentrement pour le petit et le moyen format. Sans compter divers
dispositifs pas forcément très précis, mais probablement «créatifs», permettent
d’expérimenter les bascules en petit format sur film ou silicium.
Et quant aux petites chambres de précision pour le format numérique 4,5x6 cm,
on en dénombre peut-être une douzaine, en parallèle avec un effort considérable
chez Schneider et Rodenstock pour proposer de nouvelles optiques de haute
performance dédiées à ces matériels.
Contre toute attente, décentrements & bascules qui auraient dû succomber
face à l’avancée irrésistible du progrès, les progrès de l’hydre numérique en
silicium combinée à ceux du post-traitement logiciel, eh bien ces vieilleries
mécaniques et optiques refusent de quitter la scène.
Nous proposons ici de voir pourquoi, et comment il est possible, moyennant
quelques précautions de bon sens, d’extrapoler les méthodes des bascules et
décentrements connues en grand format à l’usage du petit et du moyen format.
I Les décentrements
1) Les règles
classiques
Traditionnellement, on utilisait le décentrement pour les photos
d’architecture afin que les verticales de l’édifice photographié soient
représentées par des verticales parallèles dans l’image. Que ce soit dans la
Mission Héliographique [9] ou dans le Vieux Paris
d’Atget [10], la règle ne souffre aucune exception ; Atget
qui ne dispose pas d’objectifs à grande couverture angulaire préfère laisser
visible un vignettage en haut de certaines de ses images qui atteignent la
limite du cercle-image [11], plutôt que de laisser ses
verticales converger. On peut voir dans cette règle une survivance datant des
époques anciennes, parce que les peintres et les graveurs représentaient les
édifices de cette façon. On peut aussi arguer d’un effet physiologique qui tend
à remettre «d’apparence verticales» dans l’image rétinienne interprétée par
l’observateur les lignes verticales du monde réel délimitant les façades des
immeubles ; du moins tant qu’on ne penche pas trop la tête en arrière. Certains
souhaitent s’affranchir de ces règles strictes qui sont bien antérieures au
temps du Père Atget [6], comme on s’affranchit de la tutelle
pesante des ancêtres qui, bien entendu, brident toujours la jeunesse dans sa
créativité.
Sans entrer dans ce débat esthétique, force est de constater
qu’un certain nombre de photographes d’aujourd’hui trouvent tout de même
avantage à continuer à décentrer à la prise de vue en petit et moyen format
(numérique ou pas), même si ce n’est pas pour faire des photos d’architecture.
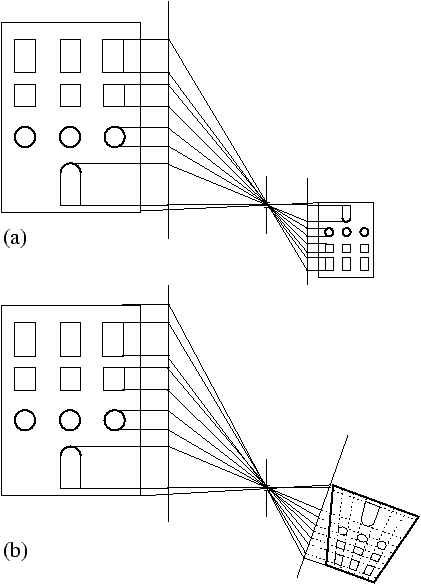
Figure 1: Le principe classique du décentrement : si le plan du film est
parallèle à la façade de l’édifice ou à la face avant du meuble (a), les
verticales se projettent verticales et parallèles dans l’image, la grandissement
est constant sur toute l’image ; si le plan du film n’est pas parallèle au plan
de la façade (b), l’image en projection centrale est affectée d’une très
classique distorsion en trapèze, les verticales convergent, le rapport de
grandissement pour une petite portion d’image varie du haut en bas de l’image
La règle classique énoncée dans les cours de photo à la chambre est très
simple (figure 1 a) : pour que les verticales de
l’édifice, ou les verticales du meuble que l’on photographie, soient parallèles
et verticales sur la photo, il faut et suffit que le plan du film (ou du
détecteur) soit gardé bien vertical et parallèle au plan de la façade de
l’édifice ou à la face avant du meuble. Et si d’aventure le plan-objet n’est pas
vertical, et si on souhaite en faire une image sans distorsion en trapèze, peu
importe finalement la verticale et la gravité terrestre, il faut et suffit en
général que le plan du film soit parallèle au plan de l’objet.
Si cette condition est respectée, du moment que la distorsion optique
intrinsèque à l’objectif est faible, l’image d’un damier à mailles carrées reste
un damier à mailles carrées, et l’image d’un cercle tracé sur le plan objet
parallèle au plan du film reste un cercle. Dès que le plan objet n’est plus
parallèle au plan image (figure1 b), l’image du damier
carré devient affectée d���une distorsion en trapèze qui est inévitable même avec
un objectif parfait, et l’image d’un cercle devient une ellipse.
Il y a en revanche un effet particulier de distorsion des sphères qui
apparaît sur le bord des images prises au grand angulaire même si le plan sur
lequel sont posées les sphères est parfaitement parallèle au film (voir figure 2).
Là encore, cet effet est inévitable et devient très visible avec les
ultra-grands angulaires. Cette déformation est gênante, par exemple, si on
photographie un groupe de personnes au grand angulaire, les visages de ceux qui
sont en bord de champ seront affectés d'un étirement peu esthétique.
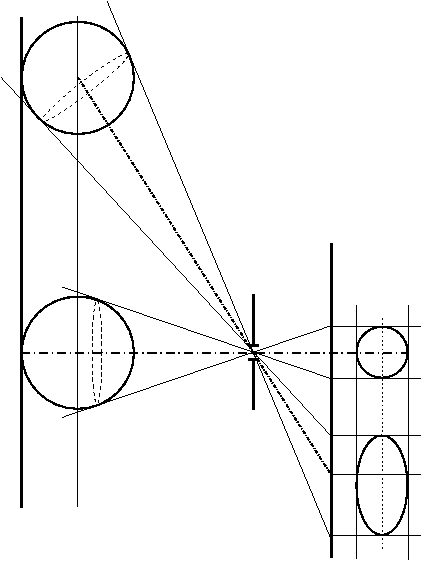
Figure 2: Même si le plan objet est bien parallèle au plan image, l’image
d’une sphère posée sur le plan objet est une ellipse d’autant plus allongée qu’on
s’éloigne de l’axe optique. La raison en est que la ligne délimitant la partie
visible de la sphère est un cercle de plus en plus incliné par rapport au plan
d’appui de la sphère, d’où la déformation en ellipse de ce contour en projection
dans l’image.
Ces règles de projection découlent directement des lois de la perspective
centrale connues depuis la Renaissance [12]. Le point-clé
de la construction géométrique étant qu’on peut simuler le rendu de
perspective photographique par un tracé de rayons analogue à celui de la
camera obscura des maîtres anciens, ou du sténopé des artistes contemporains,
en ignorant dans la plupart des cas le fait que l’objectif est composé de
verres, et qu’il n’est pas une lentille mince. Dans l’objectif photographique,
c’est la pupille d’entrée de l’objectif, c’est à dire l’image du
diaphragme donnée par la partie antérieure de l’objectif, qui joue le rôle
du sténopé dans la détermination des parties vues et cachées du sujet, et des
alignements dans l’espace objet rendus dans l’image projetée par un seul et même
point ; le rendu de perspective ne dépend que de la position de cette pupille
d’entrée par rapport à la scène photographiée et ne dépend en aucun cas de la
focale. Bien entendu, différentes focales donnent des images plus ou moins
grandes, des cadrages plus ou moins serrés, mais à l’intérieur de l’image, les
proportions relatives des objets projetés, le rendu des alignements, sont les
mêmes, à un facteur d’agrandissement près, proportionnel à la focale de
l’objectif utilisé.
On peut même étendre, sous certaines conditions expliquées dans l’annexe 1,
cette construction traditionnelle de la camera obscura au cas où les
images sont défocalisées, les formules de conjugaison de l’optique géométrique
n’étant pas une contrainte forte tant que le niveau de flou reste faible.
2) Applications
aux petits et moyens formats
En principe, le fait de travailler en petit et moyen format avec des
objectifs à décentrement prévus pour les reflex ne devrait pas changer en quoi
que ce soit cette règle classique. Nous dirons simplement que c’est presque
toujours vrai (voir annexe 1) et qu’il n’y a pas lieu dans un premier temps
de remettre en cause cette règle héritée de la photo en grand format, elle-même
héritée des règles de la perspective centrale.
On pourrait arguer que sur le terrain en quelques secondes le rendu de
perspective «correct» est obtenu par l’action d’une glissière, ce qui à l’ère de
l’image numérique épargne du temps de post-production [13].
Il est vrai que réaliser en post-production l’exact équivalent du décentrement
classique ne se ramène pas à remettre simplement les verticales convergentes
parallèles entre elles, il faut également modifier les dimensions de l’objet
dans le sens vertical par un étirement (figure 3). Pour
un détail pris avec une focale normale ou une longue focale, une simple
dilatation après correction du trapèze donne une image acceptable, mais pour une
image au grand angulaire, il faudrait que le coefficient de dilatation soit
variable du haut en bas de l’image, ce qui est difficilement accessible à un
post-traitement manuel avec les outils ordinaires du traitement d’image.

Figure 3: Il semble facile par post-traitement numérique de remettre verticales
les fuyantes d’une façade prise en contre-plongée sans décentrement. En
principe, avec une chambre à décentrement au même point de vue, le rendu de
perspective, les alignements et les parties cachées seront rendus dans l’image
projetée de la même façon qu’avec un appareil dépourvu de mouvements dont on
incline l’axe optique et dont l’image subit la distorsion en trapèze. Il n’est
pas facile, en revanche, sans avoir noté précisément l’inclinaison de
l’appareil, de déterminer après coup le dosage de la dilatation verticale
nécessaire à redonner à la façade (par distorsion inverse) ses véritables
proportions d’origine, comme dans un plan en élévation, d’autant plus que le
coefficient de dilatation à appliquer, pour une grande façade prise au grand
angulaire, devrait être variable du haut en bas de l’image à traiter.
En petit et moyen format, le décentrement s’obtient comme en grand format par
l’usage d’un objectif qui couvre nettement plus que le format de film ou de
capteur où l’image s’enregistre. Le décentrement, comme en grand format, revient
donc à un recadrage par le détecteur d’une image qui se forme excentrée par
rapport à l’axe optique. Comme les focales et les formats sont plus courts, le
déplacement mécanique nécessaire au décentrement est en proportion du
format ; il faut donc une glissière de précision.
Quel que soit le format, pour réaliser par décentrement le cadrage classique
1/3 - 2/3 à partir d’une vue où l’axe optique est centré au milieu du film ou du
capteur, il faut décentrer de 1/6 du côté du format.
Figure 4: Décentrement d’amplitude égale à un sixième du petit côté du format,
en vue de réaliser un cadrage classique 1/3-2/3
Cette valeur de 1/6 qui semble modérée et réalisable mécaniquement sans
difficultés (par exemple 4 mm pour un petit côté de 24 mm), atteint en fait
immédiatement les limites du cercle-image d’une formule optique comme un Tessar-Xenar-Planar-Xenotar
couvrant 55°-60°. En effet, sachant qu’une focale normale est égale à la
diagonale du format, pour couvrir tout le format il faut au moins 53° d’angle de
champ. Les formules optiques fameuses que nous venons de nommer, utilisées comme
focales normales, n’ont donc qu’une faible marge de couverture, en décentrant de
1/6 du côté, on atteint déjà la limite du cercle-image de l’objectif.
La plupart des adaptations permettant de décentrer un objectif qui, au
départ, n’était pas prévu pour cela, se heurtent rapidement à cette limite de
cercle-image, ce qui réduit considérablement l’intérêt de ces dispositifs. C’est
le problème qu’on rencontre, par exemple, avec les optiques Hasselblad standard
montées sur le FlexBody, d’où l’introduction de l’ArcBody équipé d’optiques de
chambre à grande couverture angulaire (100° à 120°). Aujourd’hui, les optiques
de chambre considérées comme étant «de focale normale», c’est à dire de focale
égale à la diagonale du format, couvrent entre 70° et 75° ; cet angle de champ,
par comparaison, est celui d’un 28 mm couvrant toute la diagonale du format
24x36, ou d’un 50 mm pour le 6x6.
D’où la demande pour des angles de champ plus élevés que 60°, imposant
l’utilisation de formules rétrofocus [14] devant un boîtier
reflex. Certes le rétrofocus de Pierre Angénieux [15] date
de 1950, donc ce n’est pas vraiment une nouveauté, néanmoins il était difficile
techniquement de concevoir dans les années 1950-60 une optique rétrofocus pour
appareil reflex, qui soit de grande couverture angulaire avec une faible
distorsion, alors qu’on sait faire des optiques symétriques ou quasi-symétriques
couvrant 120° depuis le début du XX-ième siècle [16], De
plus la formule symétrique permet de corriger bien plus facilement la
distorsion, mais on ne peut pas monter de tels objectifs devant un reflex parce
qu’en focales plus courtes que la diagonale du format, le miroir en percuterait
la lentille de sortie.
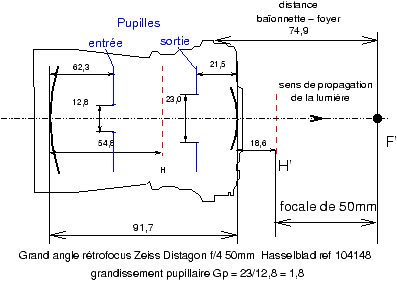
Figure 5: Une optique grand angulaire de type rétrofocus a sa dernière lentille
nettement plus loin du film que sa focale, ce qui permet le passage du miroir
reflex. Une telle combinaison optique est nécessairement dissymétrique, elle est
plus difficile à corriger des aberrations (en particulier le chromatisme
transversal, assez gênant sur capteur couleur de type Bayer) et de la
distorsion.
Les difficultés de conception optique des rétrofocus sont aujourd’hui
surmontées lorsqu’on voit, par exemple, le dernier modèle de Distagon Carl Zeiss
40 mm IF-CFE pour le 6x6, ou le modèle TS-E de 17mm à bascule et décentrement
chez Canon, ce dernier couvrant une surface nettement plus grande que le 24x36.
Il reste néanmoins que la conception même du boîtier reflex limite de
façon ultime les grands décentrements aux possibilités de déplacer la pupille de
sortie de l’objectif à l’intérieur de l’ouverture de la baïonnette, de plus
certains rayons de bord peuvent être occultés dans la chambre reflex elle-même.
Ces limitations qui n’empêchent pas de décentrer les rétrofocus de façon
utilisable dans la pratique, sous réserve de cercle-image suffisant, n’existent
évidemment pas avec une chambre non reflex. Mais il faut toujours se rappeler
qu’en montant un reflex derrière un soufflet ou derrière une chambre en vue de
décentrer et basculer, on ne pourra jamais atteindre les possibilités d’une
chambre, sauf avec des longues focales, ou en proxiphoto où les tirages de
soufflet sont toujours plus longs que la focale. C’est à dire pour des types de
prises de vues où, traditionnellement, le décentrement n’est pas une priorité
comme il peut l’être en photo d’architecture au grand angulaire.
II Les bascules
1) Les bascules
classiques du grand format
Pour voir ce qui se passe lorsqu’on bascule en petit et moyen format, il est
utile de repartir d’un exemple classique de la photo de paysage à la chambre,
qu’on appellera par commodité le Scheimpflug dans un coin.
La règle de Scheimpflug en général dit que pour que l’image soit nette après
application d’une bascule il faut réaliser les deux conditions successives :
-
il faut commencer par faire la netteté au moins sur
un point de l’objet !!
-
et tout en essayant de ne pas perdre, à la fin, la
mise au point, il faut que le plan de l’objet, le plan de l’image et le plan
de la planchette d’objectif se coupent sur une même ligne.
Remarquons qu’il n’est pas toujours facile, après avoir commencé à cadrer et
fait la mise au point sur le sujet principal (condition N°1), de régler les
bascules (condition N°2) sans perdre le réglage de netteté qu’on pensait bon.
La figure suivante (figure 6) résume la situation
finale, sans expliquer l’enchaînement des opérations permettant d’y arriver
(chaque type de chambre ou d’optique à décentrement ayant ses particularités).
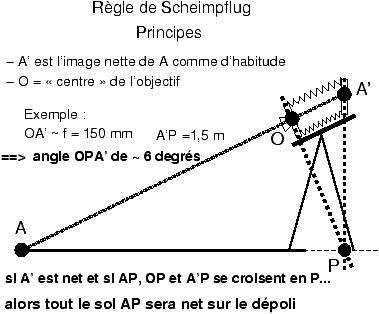
Figure 6: La règle de Scheimpflug classique du grand format
Une application pratique de ce genre de bascule est celle de la photo de
paysage avec premier plan au sol, un grand classique de l’école nord-américaine
en photographie de paysage [8]. Si on maintient le dos bien
vertical, par exemple pour que les sapins de l’arrière plan soient bien
verticaux et parallèles sur la photo, on doit respecter une construction
géométrique qui est la suivante (figure 7).
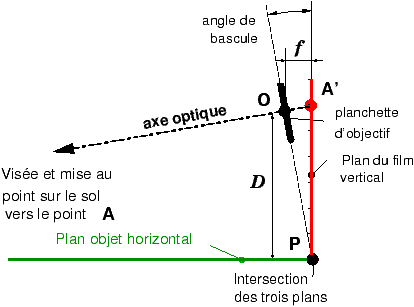
Figure 7: Épure géométrique pour la règle de Scheimpflug dans un coin ; si on
vise un objet lointain, la distance OA’ entre
le centre de la planchette et le film est proche de la focale, et les trois
plans : objet/planchette/film doivent se couper en un même point
P au sol, sous l’appareil.
Si on impose que l’image du sol se forme sur un plan vertical fixé à
l’avance, alors la seule possibilité de réglage restante en plus de la mise au
point est l’inclinaison de l’objectif, qui doit être parfaitement ajustée à la
distance à l’objet et au tirage de soufflet, afin de respecter la règle des
trois plans concourants en P, bien entendu
sans perdre la conjugaison optique entre A et
A’ qui conditionne la netteté sur le sujet
principal, par exemple le point A.
L'ensemble des positions possibles pour l’objectif, plus précisément pour le
« centre» O, point de l’axe optique au niveau
des plans principaux (en négligeant l’écart HH’
entre plans principaux comme dans une lentille mince) est donnée par la
courbe en pointillé noir sur la figure 8. Cette courbe
ressemble un peu à une hyperbole et, aux faibles angles de bascule, c’est à dire
lorsque l’appareil est placé au-dessus du sol plus haut que 4-5 fois la focale,
elle est très proche d'un simple plan vertical. Ce plan vertical est situé
environ à une fois la focale en avant du plan du film.

Figure 8: Diagramme universel du Scheimpflug dans un coin à angle droit avec
visée au sol d’un objet éloigné ; un carreau représente une fois la distance
focale f de l’objectif, ce tracé symbolique
est totalement indépendant du format couvert ; la hauteur de l’appareil et la
focale déterminent seules l’angle de bascule correct.
On peut généraliser ce diagramme au cas d’une bascule arrière (figure 9),
l’esprit reste le même, le lieu géométrique donnant toutes les positions
possibles pour le centre de l’objectif est parallèle au coin, à une distance
proche de une fois la focale, avec un léger arrondi pour la position
correspondant au rapport 1:1. L’inclinaison de la planchette est imposée par le
pivot de Scheimpflug P et la distance entre
l’objectif et le film devient très proche de une fois la focale
f dès que la hauteur au-dessus du sujet dépasse
4-5 fois la focale.
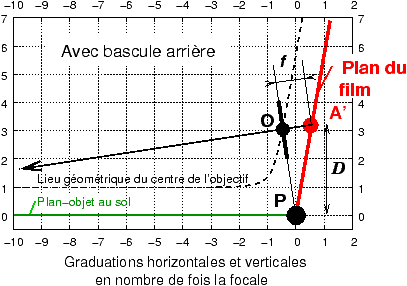
Figure 9: Diagramme universel du Scheimpflug dans un coin dans le cas d’une
bascule arrière
L’universalité du diagramme, où la focale donne l’échelle de la figure
indépendamment du format, nous permet de déterminer facilement et sans calcul
compliqué, l’angle de bascule relatif entre la planchette et le film qui fait
passer le plan de netteté de la «verticale» (ou proche de la verticale dans le
cas de la bascule arrière en paysage) à l’horizontale, au sol.
Sur les figures 7 et 9, dans le
triangle OPA’ formé par la ligne prolongeant
la planchette d’objectif et la ligne prolongeant le plan du film ou du
détecteur, le petit côté du triangle OA’ a
une longueur très proche de la focale dès qu’on place le point
O à quelques distances focales au-dessus du
sol ; les deux grands côtés de ce triangle ont des longueurs très proches de la
hauteur de l’appareil au-dessus du sol. Si on appelle D cette hauteur
au-dessus du sol, connaissant la focale f, il suffit de calculer le
rapport f/D de façon approchée et de convertir ce rapport en
valeur d’angle. La conversion s’effectue comme suit pour les petits angles
inférieurs à 20° environ : angle en degré voisin de 60°× f/D
Dans les situations photographiques courantes en paysage, ce rapport (f/D)
dépasse rarement 1/4, pour f/D=1/4 l’angle de bascule est donc de
60°/4 = 15°.
Prenons par exemple une chambre 4x5 pouces munie de son objectif «normal» de
150 mm de focale, et plaçons la chambre à 1m50 du sol ; le rapport f/D
dans ces conditions sera de 1/10, pour un angle de bascule de l’ordre de 6°,
c’est cet angle, finalement assez faible, qui suffit à faire passer le plan de
netteté (au niveau du sujet) de la verticale à l’horizontale. Notons bien que
cet angle de bascule est l’angle total formé entre la planchette et le
film, on peut l’obtenir par différentes combinaisons de mouvements sur les corps
de la chambre.
Prenons maintenant un 75 mm de focale placé à la même hauteur (que ce soit
un grand angle de chambre, ou une focale normale pour le 6x6, ou encore un
«petit télé» pour le 24x35, le problème ne dépend que de la focale et pas du
format couvert), dans ces conditions l’angle de bascule qui fait «descendre»
le plan de netteté au sol n’est plus que de trois degrés, il serait de 6 degrés
si l’appareil était placé à 75 cm du sol.
2) Les bascules en
petit et moyen format
Dans ce raisonnement, à aucun moment nous n’avons évoqué le format couvert
qui n’intervient en aucune façon. Rappelons que le rendu de perspective, la
façon dont les projections du sujet sont rendues sur le plan du détecteur, ne
dépendent que de la position de la chambre, très précisément, de la position de
la pupille d’entrée de l’objectif. La conséquence est donc très forte et
très directe pour le photographe, habitué à travailler à la chambre, qui veut
faire des photo similaires, donc avec le même rendu de perspective, en utilisant
un appareil de petit ou de moyen format avec le même point de vue sur le sujet
et la même position de pupille d’entrée pour conserver le même rendu de
perspective ; dans ces conditions, donc à hauteur inchangée au-dessus du plan du
sujet, les angles de bascules se réduisent irrévocablement en proportion
directe des focales, et donc des formats couverts si on travaille à angle de
champ identique.
Autrement dit, si on travaille toujours à 1m50 du sol, mais cette fois avec
un 28 mm de chambre sur capteur moyen format, ou avec un 17 mm en 24x36, l’angle
de bascule qui abaisse le plan de netteté à l’horizontale ne sera plus que de 1
pour 50 environ avec le 28 mm, soit à peine plus de 1 degré, et 0,6 degré
seulement avec le 17 mm !!
Sur le plan pratique, les conséquences sont immédiates : seul un dispositif
de bascule très doux et très précis permet de conserver l’effet qu’on pouvait
obtenir à la chambre. De plus, se pose le problème d’être capable d’apprécier
dans l’image l’effet de cette bascule.
Une objection qui peut venir à l’esprit à ce point de la discussion est la
suivante : sachant que les optiques dont nous parlons sont des systèmes épais,
et qu’en moyen format ou en 24x36 on aura souvent affaire à des rétrofocus dont
les plans principaux sont espacés de façon non négligeable par rapport à la
valeur de leur focale, le diagramme classique des figures 7,
8 et 9, qui néglige cette
«épaisseur optique», est-il toujours valable ? Nous renvoyons le lecteur
scrupuleux à l’annexe 2 ; de fait, le schéma est à peine modifié par une
translation séparant l’espace objet de l’espace image d’une distance égale à
l’interstice HH’ entre les plans principaux, mais en aucune façon cette
translation ne modifie les angles de bascule,
Il faut donc toujours avoir en tête cet ordre de grandeur ; en photo de
paysage à 1m50 du plan du sujet au sol, avec un 150 mm de focale, l’angle de
bascule dont on aura besoin ne dépassera sans doute jamais 6°, ce sera 3° avec
un 75 mm et environ 1° avec un 28 mm.
3) Mais en photo
rapprochée, proxi- et macrophoto, les angles peuvent rester grands
Nous avons illustré notre propos par un exemple classique en photo de
paysage, mais qu’en est-il en photo d’objets en studio, ou en photo rapprochée ?
Michel Guigue sur galerie-photo nous a offert un exemple extrême à la chambre
13x18 avec une bascule combinée (avant / arrière) de presque 60° [17].
Reprenons le diagramme de la figure 8, toujours dans
un coin à 90° et plaçons nous en position 2f-2f au rapport 1:1 : dans ces
conditions, quelle que soit la focale, l’angle de bascule sera de 45° ; et
plus généralement, en position 2f-2f dans un coin, au rapport 1:1, l’angle de
bascule sera toujours égal à la moitié de l’angle du coin (figure 10).
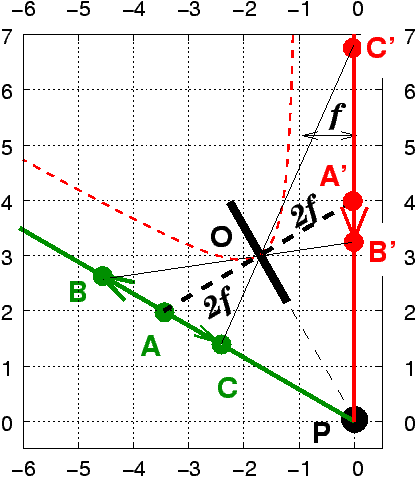
Figure 10: En position 2f-2f, soit au rapport 1:1, dans un coin, l’angle de
bascule est toujours égal à la moitié de l’angle du coin quelle que soit la
focale. Dans cet exemple où le coin forme un angle de 60°, l’angle de bascule
entre la planchette et le détecteur est de 30°. On remarque que l’objet
AB donne une image comprimée
A’B’ et que l’objet AC est fortement dilaté
en A’C’.
On remarque également la très forte compression ou dilatation de l’objet dans
le cas des grands angles de bascule en proxiphoto. La règle de Scheimpflug
concerne la netteté, mais ne dit rien de la manière dont les objets vont être
dilatés ou comprimés, c’est au photographe de contrôler son image et de décider
si le rendu est acceptable ou pas.
En pratique, l’utilisation de bascules en petit ou moyen format demande en
proxiphoto des angles de bascules nettement plus grands qu’en paysage, il n’y
aura donc pas a priori trop de problèmes mécaniques dûs à la finesse du réglage,
mais il faudra contrôler le vignettage éventuel (dans le cas d’un appareil
reflex) et surtout, bien vérifier le rendu de perspective.
4) Pourquoi des
objectifs à bascule sur berceau ?
Les utilisateurs des objectifs à bascule en petit et moyen format reflex ont
sans doute remarqué que la plupart du temps la bascule s’effectue sur un
berceau (figure 11).

Figure 11: Bascule sur berceau pour boîtier reflex
La raison en est que ce type de montage permet de faire rentrer l’axe de
rotation de la bascule à l’intérieur de la chambre reflex. De ce fait, on peut
rapprocher et même idéalement faire coïncider utilement l’axe de rotation de la
bascule avec le point nodal image N’ (ou point principal H’) situé à une fois la
distance focale en avant du foyer. Lorsqu’on bascule l’objectif autour du point
N’, les images des objets lointains se déplacent très peu dans le plan du
détecteur [18], cette façon de procéder facilite le cadrage
et la mise au point.
5) Et la
profondeur de champ avec bascules ?
Les bascules en grand format sont le plus souvent utilisées pour étendre la
profondeur de champ d’un sujet incliné par rapport à l’axe optique, il est donc
important de savoir ce qu’on peut en attendre en petit et moyen format. Nous
terminerons donc par une question des plus délicates, et qui est toujours
âprement discutée entre photographes, celle de savoir si la profondeur de champ
est plus grande en petit et moyen format en comparaison de ce qu’on obtient avec
une chambre grand format. Nous nous intéresserons pour commencer au cas de
bascules appliquées à une prise de vue d’objets à grande distance, à 10 fois la
focale et au-delà. On discutera ensuite brièvement des comparaisons de
profondeur de champ en proxiphoto et macrophoto.
a) Les
difficiles comparaisons de profondeur de champ d’un format à l’autre
L’une des raisons des malentendus sur la profondeur de champ provient de ce
que les différents contradicteurs ne considèrent pas les mêmes critères de
netteté ramenés à un même tirage final dans les mêmes conditions
d’observation lorsqu’ils cherchent à comparer les résultats obtenus en grand
format ou en petit format. À l’époque du film, on réservait souvent les travaux
à la chambre à des images de haute qualité qui pouvaient être agrandies sous
forme de grands tirages, et plus le format était petit, plus la dimension de
l’image finale était réduite. En particulier, l’apparition du grain du film aux
forts rapports d’agrandissement limitait, en général, l’utilisation des petits
formats en vue de faire de grands tirages.
Aujourd’hui que les images numériques présentent la caractéristique
extraordinaire de pouvoir être agrandies à volonté par interpolation sans faire
apparaître de grain dans les zones unies comme les ciels, la tentation est
grande de pousser les rapports d’agrandissements au-delà de la limite
traditionnelle du «grain devenant visible et gênant».
De plus, des techniques de renforcement de la netteté des images, soit par
des algorithmes secrets appliqués dans l’appareil entre la détection des photons
et la livraison du fichier au photographe, soit par des post-traitements
d’accentuation appliqués par le photographe lui-même, permettent d’envisager des
tirages de très grandes dimensions à partir de petits morceaux de silicium de
surface minuscule en regard des bons vieux plan-films.
Pour que la comparaison de profondeur de champ que nous proposons ici ait un
sens, il faut donc bien préciser les règles du jeu dans ce face à face des
différents formats :
-
on va juger de la qualité des images sur des
tirages de même dimension ; donc plus le détecteur est petit, plus le
rapport d’agrandissement optique ou numérique nécessaire sera grand ;
-
on va viser à obtenir avec des détecteurs de petit
ou moyen format des images d’au moins aussi bonne qualité que celles qu'on
obtenait en grand format sur film.
La première condition implique que les critères de netteté de l’image,
ramenés au niveau du détecteur, devront être d’autant plus serrés que le format
du détecteur est petit. La deuxième condition est encore plus sévère, elle
suppose qu’on n’aura pas de flou de bougé, et qu’on va utiliser les objectifs
dans les conditions où ils donnent leur qualité d’image maximale.
En revanche on ne va prendre en compte que les défauts de mise au point
optiques classiques qui conduisent aux limites de profondeur de champ, sans
faire intervenir ni le grain du film, ni l'application éventuelle d'un
traitement renforçateur de netteté (pour une analyse détaillée de ces problèmes,
nous renvoyons à l’article de H.H. Nasse chez Carl Zeiss [19]).
b) À grande
distance, l’hyperfocale détermine à peu près tout
Les calculs de profondeur de champ habituels sont basés sur un tracé de
rayons de l’optique géométrique et la détermination de la distance
hyperfocale classique H [20] définie par :
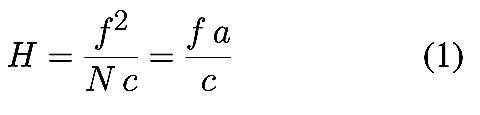
où f est la focale de l’objectif, a est le diamètre de pupille
d’entrée, N est le nombre d’ouverture défini comme N=f/a
(par exemple N = 2,8 - 4 - 5,6 - 8 - 11 - 16 - 22 - 32 …) et c est le
diamètre du cercle de confusion qui détermine le critère de netteté.
Cette distance hyperfocale H n’est pas dépendante directement du
format, mais elle en dépend indirectement via le paramètre du cercle de
confusion c en fonction du degré d’agrandissement nécessaire à
l’obtention de l’image finale.
Par exemple, sans rentrer dans les détails, si on met au point sur la
distance hyperfocale H à bascule nulle, tout sera acceptablement net
entre l’infini et la distance H/2, pour toutes les combinaisons de
focales, de nombre d’ouvertures et de cercles de confusion qui donnent la même
valeur de H.
Cette valeur de l’hyperfocale H, une fois connue, permet dans le cas
général de déterminer à partir de la distance de mise au point et de la focale
de l’objectif les limites de profondeur de champ soit en prise de vue classique
à bascule nulle (voir ces articles sur galerie-photo.com [21],
[22]), mais permet également de déterminer les zones de
netteté limite lors de l’application d’une bascule [23].
Autrement dit, une fois la valeur de l’hyperfocale déterminée, les zones de
netteté, pour un point de vue donné, sont déterminées indépendamment du format.
De plus, à grande distance, les zones de profondeur de champ ne dépendent
pratiquement plus de la focale de l’objectif (voir l’annexe 3), seul importe la
distance de mise au point et la valeur de l’hyperfocale H.
Le tableau ci-dessous donne les valeurs traditionnelles pour c,
choisies pour qu’un tirage agrandi à la même dimension finale d’environ 20x25 cm
pour les différents formats de film ou de détecteur qu’on veut comparer, et
observés à 30 cm de distance, satisfasse les critères de haute résolution.
Traditionnellement, pour des raison physiologiques, on choisit comme
dimension angulaire pour le plus petit détail discernable un angle de 2 minutes
d’arc ; ces deux minutes d’arc correspondent en radians à 2/(60x57), la valeur
de c est donc de l’ordre de (diagonale du format)/1720 pour 2 minutes
d’arc vues à 30 cm). Table des valeurs traditionnelles du cercle
de confusion, pour une observation visuelle d’un tirage de dimensions
20x25 cm à 30 cm de distance et une limite angulaire de résolution de 2
minutes d’arc
| |
|
valeur c du cercle de confusion |
| |
|
pour une limite angulaire |
|
format initial |
diagonale |
de deux minutes d’arc |
|
film ou capteur |
du format (mm) |
en observation visuelle à 30 cm |
| |
|
pour un tirage de dimensions 20x25 cm |
| |
|
|
|
20x25 cm |
300 mm |
170 microns (tirage-contact) |
|
4x5 pouces (10x12,7 cm) |
150 |
85 microns (agrandir 2x) |
|
6x9 cm (56x82 mm) |
100 |
58 microns (agrandir 3x) |
|
6x6 cm (56x56 mm) |
80 |
46 microns (agrandir environ 3x-4x) |
|
24x36 mm |
43 |
25 microns (agrandir 6,5x) |
|
18x24 mm ou APS-C |
≃ 30 |
17 microns (agrandir 10x) |
|
four-thirds |
21 |
12 microns (agrandir 14x) |
Dans cette approche, on voit tout d’abord que les valeurs de cercle de
confusion sont totalement dépendantes des règles d’observation ; pour
chaque application photographique, il faut donc, en principe, recalculer cette
table en fonction du mode d’observation final choisi. Si une règle du jeu
supplémentaire précise que les tirages devront être de dimension 40x50 cm
observés à 30 cm (ce qui rend difficile la vision globale du tirage),
alors il faudra diviser par deux toutes les valeurs du tableau précédent ; et si
c’est un tirage d’album de famille dans le genre 10x15 cm qui est le but
recherché, on pourra à l’inverse multiplier par deux toutes les valeurs. Si la
règle dit : tirages 40x50 cm, mais pour une exposition où le public ne devra pas
s’approcher à moins de 60 cm du tirage, alors on conservera les valeurs
inchangées.
Dans tous les cas, la dimension effective du diamètre de cercle de confusion
c est en proportion directe de la diagonale du format, une fois appliquée
la règle n°1 de notre jeu comparatif ; à angle de champ constant d’un format à
l’autre, cette valeur de c sera donc proportionnelle à la focale
utilisée. La conséquence est que dans la comparaison entre formats, si on
applique le critère de netteté sur la même image finale, le rapport (f/c)
ne change plus dans le calcul de l’hyperfocale H=(f2)/N.c)
=(f/c).(f/N), il ne reste qu’un changement
éventuel du rapport (f/N).
Appliquons alors la règle du jeu N°2 : recherche de la meilleure qualité de
l’image optique. Il se trouve que tous les objectifs de haute performance
utilisés en petit format, moyen format et à la chambre possèdent un meilleur
diaphragme en-deçà duquel la qualité d’image s’améliore en diaphragmant (par
réduction progressive des aberrations géométriques résiduelles), mais
au-delà duquel la qualité d’image se dégrade à nouveau par effet de diffraction.
Ce meilleur diaphragme, pour les optiques classiques de l’époque du film c’est
par exemple : f/5,6 pour le 50 mm normal du 24x36, f/8-f11 pour une optique
standard 75-80 mm du 6x6, f/11-f/16 pour un 100 mm standard du 6x9, f/22 pour un
150 mm standard du 4x5 pouces, f/32-f/45 pour un 300 mm standard du 20x25 cm,
etc …
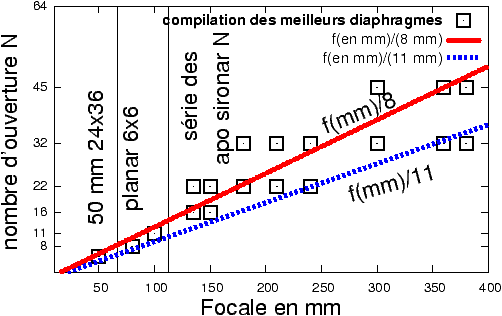
Figure 12: Compilation des meilleurs diaphragmes pour les optiques de focale
normale fixe, de petit, moyen et grand format, couvrant entre 50° et 75° d’angle
de champ ; les optiques classiques ont un meilleur diaphragme qui suit
approximativement la loi : meilleur diaph = focale (en mm) / 8 mm ; pour les
optiques de très haut de gamme les plus récentes, ce serait plutôt : meilleur
diaph = focale (en mm) / 11 mm.
La tendance suit approximativement une loi d’échelle simple :
Optiques classiques de focale
normale ;
Nopt =
meilleur nombre d’ouverture = focale en mm/8 mm
Optiques de focale normale les
plus modernes ;
Nopt =
meilleur nombre d’ouverture = focale en mm/11 mm
Cette compilation montre que le meilleur diaphragme, l’optimum, Nopt,
pour des optiques standard d’angles de champ comparables, du format 24x36 mm au
20x25 cm, est donné par un rapport (f/Nopt) = constante, entre
8 et 11 mm. Utilisées au meilleur diaphragme Nopt, les
optiques comparables d’un format à l’autre vont donc travailler dans des
conditions où le rapport (f/Nopt) est constant ; cette
condition, jointe à la condition de proportionnalité du cercle de confusion c
à la focale, ont pour conséquence que les différentes prises de vue et
agrandissements vont s’effectuer à hyperfocale constante.
Autrement dit, utilisés au meilleur diaphragme, tous les objectifs
standard d’angles de champ comparables donnent la même distance hyperfocale,
donc pour un objet pris du même point de vue, donneront la même profondeur de
champ si l’observation visuelle s’effectue sur un tirage final de mêmes
dimensions.
c) Et si on
bascule ?
Si on bascule, la zone de netteté acceptable côté objet, autour d’un point de
visée (A) ou (C) dont les images nettes sont (A’) et (C’) est comprise entre
deux plans-limites (L1 PF) et (L2 PF) formant un coin. Ce
coin est déterminé par les règles suivantes (figure 13) :
-
le plan-objet contient les points (L), (A), et (P),
(P) étant le pivot de Scheimpflug sous l’objectif, à une distance h
vers le bas, comme expliqué précédemment ;
-
le plan-image contient les points (P), (A’), (C’)
de façon que (A’) soit l’image nette de (A) le long de l’axe optique ; la
règle de Scheimpflug étant respectée via la conjugaison (A A’) et le pivot
(P), l’image nette du plan (A C P) est le plan (P A’ C’) ;
-
sur l’axe optique, les points (P1) et (P2) donnent
les limites de profondeur de champ classique qu’on obtiendrait sans
bascule ;
-
en avant de la lentille, à la verticale sous le
foyer-objet (F), dans le plan (A C P), on place un point (PF) qui sera le
pivot du coin de profondeur de champ ; ce point (PF) est distinct du pivot
de Scheimpflug (P), mais il en est relativement proche car l’hyperfocale
H est en pratique toujours beaucoup plus grande que la focale f ;
-
sur l’axe optique à une distance égale à une fois
l’hyperfocale H, on place un point (L0) :
-
à la verticale de (L0) on place un point (L) sur le
plan objet incliné (L A C P) ;
-
au-dessus de (L), à une distance verticale égale à
h, on place un point (L1) et en-dessous de (L) à la même distance
verticale h on place un point (L2) .
-
le coin d’espace défini par les plans (L1 P1 PF)
et (L2 P2 PF) autour du plan-objet (L A PF P) définit la
zone de netteté
acceptable.
Comme la distance hyperfocale est toujours très grande devant la focale
(ce qui équivaut à dire que le diamètre de pupille d’entrée est toujours très
grand devant le diamètre du cercle de confusion, par exemple avec un 150 mm de
chambre à f/16, la pupille d’entrée a un diamètre de l’ordre du centimètre, pour
un cercle de confusion de l’ordre de 0,1 mm, soit un facteur 100), la
figure 13 ne change pratiquement pas si la focale f
varie à distance hyperfocale H constante; donc la profondeur de champ à
hyperfocale constante est inchangée, même avec bascules.
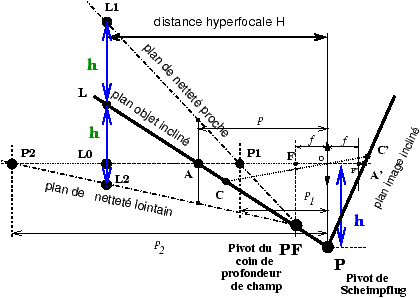
Figure 13: D��termination de la profondeur de champ avec
bascules pour une hauteur h de la chambre au-dessus du plan-objet incliné
et une distance hyperfocale H ; le coin est formé par les plans
(L1 P1 PF) et (L2 P2 PF) autour du plan-objet (L A PF P).
La figure 14 explique la situation : si la focale
est, par exemple, divisée par deux, le point (A’) image de A se rapproche de
l’objectif, à peu près deux fois plus proche si (A) est au-delà de 10 fois la
focale ; l’angle de bascule diminue, à peu près d’un facteur 2 ; mais si on
suppose que ni la hauteur h où on place la chambre ni l’hyperfocale H
ne changent, le seul changement est une toute petite modification du coin par
suite du petit déplacement du pivot de profondeur de champ (PF) qui se rapproche
de l’objectif.
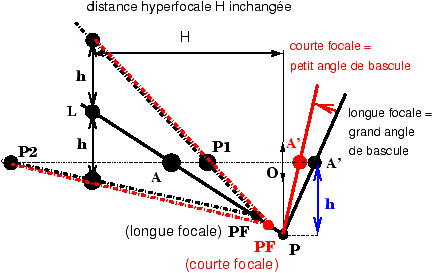
Figure 14: Lorsqu’on conserve le même point de vue pour le point (O), donc la
même distance AO à l’objet, la même inclinaison du plan-objet (L A PF P), la
même hauteur OP = h au-dessus de ce plan, à distance hyperfocale H
constante, le changement de la focale f ne modifie pratiquement pas la
zone de netteté ; en revanche l’angle de bascule côté image se réduit en
proportion directe de la focale.
Les conséquences sont donc directes :
-
Choisir de travailler avec des focales plus courtes
à angle de champ constant, par exemple sur un capteur de petites dimensions
pour obtenir la même netteté qu’à la chambre est possible, mais il ne
faut pas espérer de gain en profondeur de champ si on vise des images au
maximum de la qualité possible ;
-
Les angles de bascule, pour les objets lointains,
se réduisent en proportion directe des focales et donc des formats, ce qui
exige un système de réglage de bascule très sensible et très précis ;
-
L’appréciation sur un petit dépoli de la netteté
avec bascules devient très difficile, surtout avec les objectifs
grand-angulaires, mais en visée vidéo directe agrandie sur un moniteur, si
le dos le permet, on retrouvera le confort du dépoli d’une chambre grand
format et on pourra régler les bascules visuellement sur le moniteur si les
mécanismes de bascule de l’appareil sont assez précis.
d) Quelques
mots sur la proxiphoto et la macrophoto
En proxiphoto et en macrophoto, avec un appareil ordinaire à bascule nulle,
la profondeur de champ à diaphragme donné ne dépend pratiquement que du
grandissement (voir annexe 3). On n’a donc aucun gain en profondeur de champ à
utiliser des courtes focales dans ces conditions. Classiquement en 24x36,
bien qu’il existe d’excellents objectifs dont la focale est proche du 50 mm
standard, on utilise également des focales «macro» nettement plus longues entre
100 et 200 mm. Avec de telles focales, en ajoutant le tirage de soufflet
nécessaire à faire la mise au point pour des grandissements se rapprochant de
l’unité, l’usage des bascules en montant un boîtier reflex sur un soufflet ou
sur une chambre ne posera pas de problème mécanique particulier. Nous ne
discuterons pas en détail du tracé de la zone de profondeur de champ, qui obéit
au règles énoncées précédemment, mais dont il n’est pas facile de tirer des
conclusions simples.
Il faut tout de même se rappeler que lorsqu’on est au rapport 1:1, G=1,
le nombre d’ouverture effectif Neff = N∞(1+G)
double par rapport à la position infini-foyer. La conséquence sur le temps de
pose est bien connue, le facteur de soufflet correcteur de pose est (1+G)2 ;
par exemple au rapport 1:1, G=1, G+1=2, le coefficient
prolongateur de pose est de 4x, équivalent à ouvrir de 2 crans de diaphragme.
Mais ce doublement du nombre d’ouverture effectif a une conséquence analogue sur
la limite de résolution dans l’image, due à la diffraction ; la dimension de la
tache-image de diffraction étant de l’ordre de Neff
microns. Autrement dit, si on ferme à f/11, au rapport 1:1 on aura un effet de
diffraction analogue à celui qu’on aurait à l’infini à f/22. Maintenir une très
haute qualité d’image, indépendamment des problèmes de stabilité mécanique et de
vibrations, impose un compromis sévère entre la profondeur de champ et le piqué
de l’image ; une bascule est donc très utile pour rattraper la netteté sur un
objet incliné, mais quasi-plat.
Une solution par post-traitement numérique, qui balaye d’une certaine façon
toute la discussion procédente sur les zones de netteté entre plans inclinés,
consiste à réaliser une fusion d’images enregistrées à différentes distances de
mise au point, en ne retenant que le plus net de chaque prise. Comme toutes les
techniques numériques qui apparaissent à première vue comme des «méthodes de
force brute», l’évolution de l’informatique depuis l’époque des élégantes cartes
perforées 80 colonnes et des superbes bandes magnétiques demi-pouce nous incite
à accepter que bien souvent, au détriment de l’élégance, la force brute finit
par s’imposer.
Résumé et Conclusions
En Résumé :
-
Les décentrements ne posent aucun problème
particulier en petit ou moyen format sauf si on espère travailler avec un
grand angulaire et un boîtier reflex, auquel cas les possibilités de
décentrement, à cause des vignettages dûs au boîtier, sont nettement plus
limitées qu’avec une petite chambre non reflex équipée d’une optique
grand-angulaire quasi-symétrique ;
-
Dans la course à la performance optique en grand
angulaire, les objectifs de chambre quasi symétriques, non utilisables sur
un reflex, font l’objet de développements récents poussant la qualité
d’image à un niveau inattendu, la compétition avec les rétrofocus n’est pas
terminée bien au contraire, les optiques quasi-symétriques de très courtes
focales permettant, en valeur relative, la même gamme de décentrements qu’en
grand format ;
-
Avant de dire qu’on peut avoir un gain en
profondeur de champ en travaillant sur petit capteur avec des courtes
focales, il faut déjà savoir quel niveau de qualité d’image on souhaite
atteindre ; atteindre le niveau de ce qu’on obtient sur film en grand format
impose des contraintes très fortes sur la profondeur de champ effectivement
utilisable avec un petit capteur, et en travaillant au meilleur diaphragme,
d’un même point de vue, le gain n’est pas forcément possible ;
-
L’application d’une bascule permet de récupérer la
profondeur de champ sur un objet incliné, mais quasi plat, ou du moins :
rentrant à l’intérieur d’un coin ; l’utilisation de courtes focales, d’un
même point de vue et à distance hyperfocale identique, en vue d’images de
haut de gamme, n’apporte pas de gain en profondeur de champ ; côté image,
les angles de bascule se réduisent en proportion directe de la focale ; et
on ne peut absolument pas négliger des angles mêmes très petits si on a
l’ambition d’égaler ce qu’on obtient en grand format avec une grande focale
et un grand angle de bascule facile à régler ;
-
La fusion numérique d’images prises à différentes
distances, avec un balayage en profondeur, permet en principe de
s’affranchir de réglages de bascule en donnant par calcul a posteriori
une profondeur de champ … à volonté, ou presque ; mais cette approche repose
sur un post-traitement informatique lourd qui pour l’instant est peut-être
encore plus coûteux en temps de travail que le réglage de l’objectif à la
prise de vue : affaire à suivre, car il suffit de se rappeler ce qu’étaient
les systèmes de prise de vue et de post-traitement numériques il y seulement
10 ans ...
Remerciements
Cet article n’existerait pas sans les très nombreuses discussions du forum
http://galerie-photo.info qui ont
accompagné la mutation de la prise de vue depuis ces 10 dernières années. On a
beaucoup parlé de la quête de la netteté et de la profondeur de champ ultimes,
ainsi que des possibilites réelles ou rêvées de monter un boîtier reflex 24x36
sur une chambre.
Parmi les contributeurs réguliers du forum, merci à Jean-Paul Planchon pour
avoir fait partager sa découverte de l’étrange distorsion en trapèze des
objectifs rétrofocus, qui font mentir les cours classiques de photo à la
chambre, et merci à Fabrice pour avoir donné l’explication et la simulation du
phénomène.
Annexe 1 : Lorsque les rétrofocus
distordent en trapèze !
La règle classique permettant de conserver verticales et parallèles les
lignes d’un édifice lorsqu’on travaille à la chambre ne met pas a priori
de condition très stricte sur l’orientation de l’objectif. La règle de
Scheimpflug oblige à ce que le plan de l’objet, la planchette d’objectif et le
film soient parallèles pour que l’image soit nette. On est cependant libre de
basculer un peu l’objectif sans avoir de la distorsion en trapèze, mais en
perdant la netteté parfaite, lorsqu’on veut absolument basculer l’objectif entre
un plan objet et un plan image parallèles entre eux. Par exemple pour pointer
l’appareil vers le haut de l’édifice.
De fait, et c’est très subtil, cette tolérance sur l’inclinaison de
l’objectif n’est applicable qu’avec les objectifs de chambre qui sont presque
tous de construction quasi-symétrique. Avec les grands angulaires rétrofocus
pour petit et moyen format reflex, même si le plan de l’objet et le plan du
détecteur sont parallèles, le fait de basculer l’axe optique fait non seulement
perdre la netteté (effet classique) mais introduit une distorsion en trapèze
supplémentaire qui n’existe pas avec les optiques symétriques ou
quasi-symétriques. La raison en est subtile ; lorsqu’on bascule l’objectif
entre des plans objet et film qui sont parallèles, l’image qui se forme n’est
plus une image nette mais une pseudo-image issue de la projection défocalisée du
diaphragme sur le détecteur. Or les optiques grand angulaires rétrofocus ont la
particularité d’avoir leurs pupilles qui ne sont plus situées au voisinage des
points nodaux (ou principaux) comme dans les optiques de chambre. Cette
particularité induit une distorsion supplémentaire en trapèze qu’il est très
difficile d’appréhender sans faire une simulation par un tracé de rayons. Dans
la pratique cet effet n’apparaît que très rarement, car il est rare de décentrer
et de basculer simultanément avec les objectifs spéciaux prévus pour le 24x36.
|
Vue de côté
|
Vue de dessus
|
|
(a) Tracé de rayons entre plans parallèles, optique inclinée avec
pupilles dans les plans principaux ; la simulation de ce système
s’effectue avec une «lentille aplanétique» infiniment mince, diaphragmée
en son centre.
|
|
(b) L’image d’une grille n’est pas déformée si on incline une optique
symétrique dont les pupilles sont aux plans principaux.
|
|
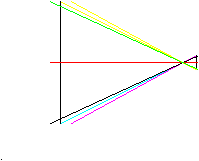
Figure 15: Dans les cours classiques de photo à la
chambre, on apprend qu’on peut incliner un peu l’objectif entre un plan
objet et un plan image parallèles sans que la distorsion en trapèze
n’apparaisse : c’est vrai pour les optiques quasi-symétriques dont les
pupilles sont proches des plans principaux.
|
|
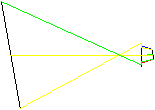
Vue de côté |
Vue de dessus |
|
(a) Tracé de rayons entre plans parallèles, optique inclinée avec
pupilles loin des plans principaux ; la simulation de ce système
s’effectue avec une «lentille aplanétique» infiniment mince, diaphragmée
en un point situé loin de son centre.
|
|
(b) Contre toute attente, l’image d’une grille est déformée si on
incline une optique dissymétrique dont les pupilles sont loin des
plans principaux ; c’est un effet tout à fait inhabituel, inconnu au
sténopé et inconnu dans la tradition des optiques grand angulaires
de chambre quasi-symétriques, mais qui existe avec les grand
angulaires rétrofocus !
|
|
Figure 16: Effet de distorsion
spécifique aux grands angulaires rétrofocus lorsqu’on penche
l’objectif entre plan objet et plan image parallèles
|
Annexe 2 : Règle de Scheimpflug avec une
optique épaisse
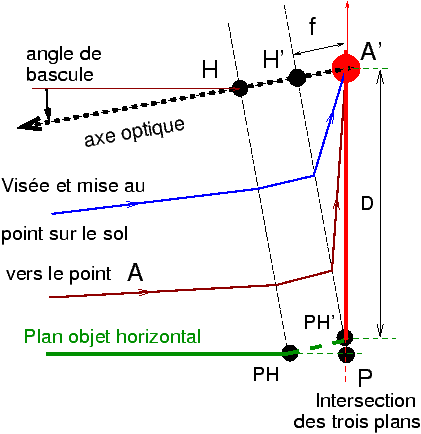
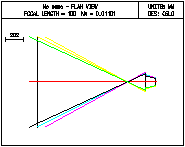
Figure 17: Règle de
Scheimpflug avec une optique ��������paisse
Pour se représenter ce qui se passe dans une optique épaisse, il suffit, en
repartant de la figure 7 d’imaginer qu’on écarte l’espace
objet de l’espace image en coulissant l’espace image le long de l’axe optique
d’une quantité égale à l’interstice HH’, qui est la
distance entre les plans principaux (pour plus de détails sur les tracés de
rayons dans une optique épaisse, nous renvoyons à l’article [18]
sur galerie-photo.com).
L’angle de bascule est inchangé puisqu’on déplace l’espace image
parallèlement à l’axe optique sans aucune rotation. La construction se complique
un peu puisqu’au lieu d’un seul pivot de Scheimpflug P,
on doit tracer trois points PH, PH’ et P et prendre
en compte le triangle (H’ PH’ P ). Pour
déterminer le point PH’, il suffit d’imaginer un
hypothétique rayon lumineux cheminant le long plan objet et qui doit sortir le
long du plan image ; le segment PH PH’ est
parallèle à l’axe optique et il est égal au segment HH’.
Comme l’interstice HH’ est en général très faible
devant la distance focale f, la construction simplifiée de la figure 7
suffit presque toujours.
Annexe 3 : Formules de profondeur de champ
à grande distance et en proxi ou macrophoto
Les formules classiques de la profondeur de champ entre plans (objet/image)
parallèles sont les suivantes. Après avoir déterminé la valeur de la distance
hyperfocale H=f2/N c = f a/c
, où f est la focale de l’objectif, a est le diamètre de pupille
d’entrée, N est le nombre d’ouverture défini comme N=f/a
et c la valeur du diamètre du cercle de confusion, on choisit la distance
de mise au point p. Dans les formules ci-dessous, la distance p
n’est pas mesurée par réf��rence au plan du film, comme c’est souvent le cas sur
les bagues de mise au point des appareils classiques, p est mesurée à
partir de la position du plan principal objet H de l’objectif. Dans la
pratique, H se situe au milieu de l’objectif dans les formules
quasi-symétriques. On détermine alors la distance la plus proche donnant une
netteté acceptable, p1 ; et on détermine p2
la distance la plus lointaine donnant une netteté acceptable. Tout ce qui se
situe entre p1 et p2
dans l’espace objet sera rendu acceptablement net sur la photo.
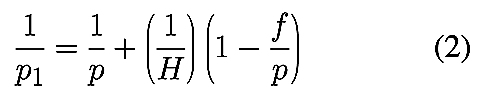
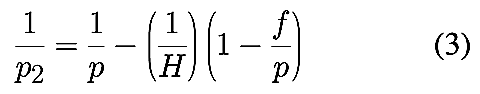
À grande distance
Lorsque la distance p devient grande devant la focale, par exemple
p>10f, le terme supplémentaire en f/p devient
négligeable, et les formules se simplifient :
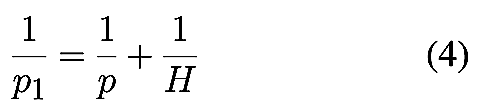
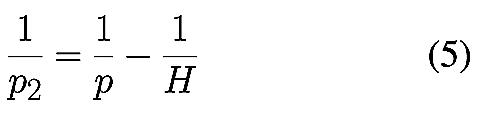
Dans ces conditions, la profondeur de champ ne dépend plus que de la distance
de mise au point p et de la valeur de l’hyperfocale H. La
dépendance vis à vis du format ou la dépendance directe à la focale
disparaissent.
En proxi et en macrophoto
Il est possible de récrire les équations (2) et (3)
en remplaçant p en fonction du grandissement G :
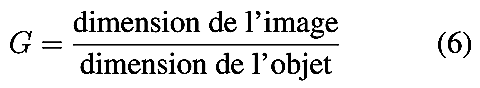
Rappelons tout d’abord une formule très utile en proxi et macro-photo qui
relie le grandissement G à l’extension «ext» de tube, de rampe
hélicoïdale ou de soufflet au-delà du foyer, pour une focale f :

Cette expression est générale quelle que soit la combinaison optique, en
particulier même si on a affaire un un télé-objectif ou un rétrofocus. Cette
expression (7) est à associer avec celle reliant la
distance p entre l’objet et l’objectif (de fait, c’est la distance au
plan principal H) avec le grandissement G, qui est une autre façon
d’exprimer la formule de conjugaison de Descartes, du moins la version
«photographique» avec objet réel et image réelle, dans laquelle toutes les
quantités p,p′,f,G sont positives :
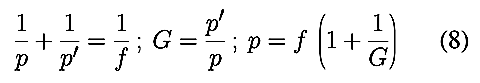
La distance totale Dtot entre l’objet et l’image s’écrit,
dans le cas général, en tenant compte de la distance HH′ entre plans
principaux :
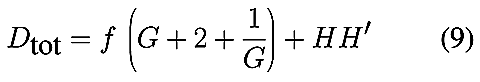
Dans la plupart des cas, on peut, en valeur relative vis à vis de la focale,
négliger l’interstice HH′ ce qui simplifie l’expression précédente (9) :
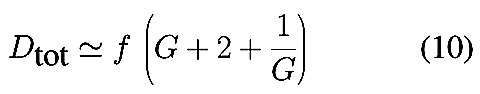
Par exemple, si G=0,1, on est au grandissement 1:10, l’objet se trouve
à (1+10) = 11 fois la focale en avant de l’objectif, l’extension de tirage
au-delà du foyer est de 0,1 fois la focale, la distance totale (objet-film) est
de l’ordre de 12,1 fois la focale.
Exprimées en fonction du grandissement G, les formules de profondeur
de champ (2) et (3) se mettent sous la
forme suivante ;
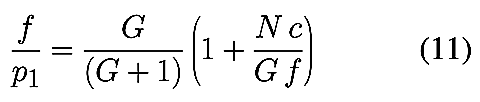
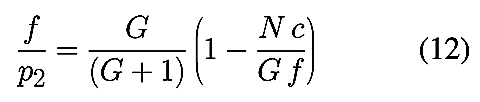
Si le terme N c/G f devient très petit, c’est à
dire si G ~ N c/f, les expressions (11)
et (12) permettent, en remplaçant 1/(1 ± N c/G f)
par une valeur approchée (1 ± N c/G f), de trouver
une expression très simple de la profondeur de champ valable en proxi et
macrophoto, qui ne dépend plus explicitement ni de la focale ni des distances au
sujet ou à l’objet :
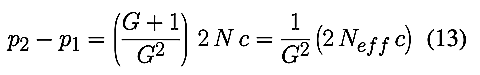
En particulier si G=1 au rapport 1:1, on retrouve l’expression
classique de la profondeur de champ totale dans cette situation : p2
− p1 = 4 N c = 2 Neff
c.
Examinons rapidement le domaine de validité de la formule (13).
Prenons N=16, c=50 µm comme traditionnellement en 6x6, f=120 mm,
la condition G ≫ N c/f implique 1/G ≪ 120/16
× 0,05 = 150 ; prenons par exemple G<1/10, la condition est largement
réalisée, ce qui veut dire en pratique que dès qu’on doit utiliser une allonge
de soufflet dépassant le dixième de la focale, l’expression (13)
est la bonne et que la focale n’intervient plus dans la profondeur de champ à
diaphragme donné, c’est le grandissement G qui l’impose.
Il n’y a donc aucun gain en profondeur de champ à vouloir utiliser des
courtes focales en macrophoto. L’usage de focales longues donne plus de distance
au sujet ce qui facilite les éclairages ; on a également des distances à l’objet
plus grandes, ce qui facilite l’application éventuelle de bascules. Des focales
trop longues conduisent en revanche à des montages moins compacts et plus sujets
aux vibrations, l’un des problèmes majeurs de perte de netteté surtout pour G>1.
Références
|
[1] |
René Bouillot : Moyens et grand formats,
Paul Montel (1971)
|
|
[2] |
-
René Bouillot : L’objet et son image.
Photographie industrielle et publicitaire, Paul Montel (1978)
|
- [3]
|
-
Pierre Groulx : Photographie en grand
format, Modulo, Québec (2001), ISBN 2891135059
|
|
[4] |
(en anglais) Leslie D. Stroebel,
View Camera Technique, 7-th Ed., Focal Press (1999), ISBN 0240803450
|
|
[5] |
(en anglais) Harvey Shaman, The
View Camera: Operations and Techniques, Amphoto Books (1992), ISBN
0817463755
|
|
[6] |
On notera néanmoins que les règles classiques sur
le rendu des verticales sont aujourd’hui bien respectées dans les
publicités immobilières, où apparemment le client a toujours peur de
voir les murs de sa future résidence lui tomber dessus ; ainsi que
chez les fabricants de meubles, toujours attentifs à ce que l’image
de leurs produits soient parfaitement conformes à la norme de la
photographie professionnelle à la chambre.
On cherchera vainement une justification scientifique à cette
nécessité classique de rendre les verticales parallèles dans les
images, alors qu’on accepte de voir converger les fuyantes sur un
sol horizontal représenté en peinture ou en photographie
d’architecture. Acceptons que la raison en est plutôt culturelle ou
physiologique, et qu’il en va de cette convention
(qui remonte même plus loin que la perspective centrale de la
Renaissance : dans la perspective cavalière du Moyen-Âge, les
verticales ne convergent pas non plus) comme il en va de la
fameuse illusion du diamètre apparent de la Lune. La vision
de la pleine Lune à son lever à l’horizon nous la fait voir bien
plus grosse qu’elle n’est en réalité ; à part quelques minuscules
effets de réfraction qui auraient, au contraire, tendance à
l’aplatir, son diamètre apparent reste obstinément proche de 1/2
degré d’angle. On la «coincera» avec précision entre deux clous
distants d’environ 1 cm placés à 1m20 du point de visée, que la Lune
se lève l’horizon ou qu’elle soit isolée au milieu du ciel étoilé et
loin de tout repère terrestre. Les publicités dans lesquelles il
faut montrer une belle grosse lune sont donc, soit prises avec un
objectif dont l’angle de champ est au maximum de quelques degrés
(soit une focale de plus de 500 mm en format 24x36), soit sont des
images composites où la Lune est rajoutée artificiellement,
justement pour respecter cette convention, ou cette illusion.
|
|
[7] |
Theodor Scheimpflug (1865 - 1911) est un
officier autrichien à qui on doit en 1904 un brevet fondateur sur la
formation d’images photographiques nettes entre plans inclinés. Son nom
reste attaché à la règle des trois plans, bien qu’un brevet britannique
antérieur de Jules Carpentier propose un principe identique pour le tirage à
l’agrandisseur.
Carpentier, Jules. Improvements in Enlarging or like Cameras.
brevet britannique N°1139 (1901)
Le texte du brevet de Carpentier :
http://www.trenholm.org/hmmerk/CARPNTR.pdf
Scheimpflug, Theodor. Improved Method and Apparatus for the Systematic
Alteration or Distortion of Plane Pictures and Images by Means of Lenses and
Mirrors for Photography and for other purposes, brevet britannique N°
1196 (1904)
Le texte du brevet de Scheimpflug :
http://www.trenholm.org/hmmerk/TSBP.pdf
|
|
[8] |
Ansel Adams (1902 - 1984) célèbre photographe
californien, qui, en plus de son travail d’artiste, a rédigé plusieurs
ouvrages didactiques sur la technique photographique. Dans l’ouvrage The
Camera, on trouvera des exemples détaillés de l’utilisation des
mouvements de la chambre en photo de paysage.
Ansel Adams, The Camera, Bulfinch (1995) ISBN 0821221841
Voir également : Examples: The Making of 40 Photographs, Bulfinch
(1989) ISBN 082121750X
|
|
[9] |
Anne de Mondenard, La Mission
héliographique, cinq photographes parcourent la France en 1851, Éditions
du Patrimoine (2002), ISBN 2-85822-690-3
|
- [10]
|
Laure Beaumont-Maillet, Atget Paris, Hazan
(2003), ISBN 2850252948
Jean-Claude Lemagny, Sylvie Aubenas, Pierre Borhan, Luce Lebart,
Atget le pionnier, Marval (2000), ISBN 2-86234-298-X
|
|
[11] |
Exemples de vignettage dans les photos
d’Atget :
http://www.johncoulthart.com/feuilleton/wp-content/uploads/2006/07/atget1.jpg
http://www.ultrapdx.com/zero/wp-content/uploads/2008/01/rauschenberg_ultra.jpg
|
- [12]
|
Denis Favennec, en collaboration avec
Emmanuel Riboulet-Deyris, Douce perspective. Une histoire de science et
d’art, Ellipses (2007), ISBN 978-2-7298-3399-2
|
- [13]
|
Avant le traitement numérique, il était
possible à l’agrandisseur de «redresser les perspectives» par une
combinaison judicieuse de l’inclinaison du plateau, de l’objectif et du
film. Une simple inclinaison du plateau permet de redresser les perspectives
mais en perdant la netteté, le réglage le plus complet combine une
inclinaison du plateau avec l’inclinaison de l’objectif et du porte-film
pour respecter la règle de Scheimpflug.
|
- [14]
|
Le terme de rétrofocus, dû à la firme Angénieux,
désigne une optique grand angulaire dans laquelle la distance entre
la dernière lentille et le foyer (donc, le film, là où se forme
l’image si on fait des photos à grande distance) est nettement plus
grande que la focale de l’objectif. Dans tous les objectifs de
chambre ou dans les objectifs de focale normale des reflex, cette
distance est soit proche, soit plus petite que la focale de
l’optique. Ce qui interdit de monter des optiques analogues aux
optiques grand angulaires de chambre sur les boîtiers reflex. Il se
trouve que les principes de symétrie aident considérablement à la
conception des grands angulaires de haute performance, et sont
connus depuis la fin du XIX-ième siècle. Si on prend l’exemple du
Biogon de chez Zeiss, pour arriver à faire aussi bien que cette
formule quasi-symétrique datant des années 1950, il a fallu trois
générations des rétrofocus Distagon et trois décennies successives
de recherche et développement dans le même bureau d’études optiques
pour arriver à égaler les performances du Biogon, tout en restant
plus volumineux. Les optiques grand angulaires équipant les boîtiers
24x36 non reflex (viseur optique ou électronique, télémètre,
…) bénéficient des mêmes avantages que les optiques de chambre,
compacité et performance grâce au principe de symétrie.
|
|
[15] |
Angénieux, Pierre (1907 - 1998) ingénieur et
chef d’entreprise français, grand concepteur d’optiques à qui on doit la
formule rétrofocus : objectif dont la distance focale est nettement plus
courte que la distance entre la dernière lentille et le foyer. Les
rétrofocus sont en général caractérisés par une pupille de sortie de plus
grand diamètre que la pupille d’entrée, le grandissement pupillaire pouvant
dépasser 2 dans certaines optiques pour le format 24x36.
|
|
[16] |
Par exemple, l’Hypergon de chez Goerz,
breveté au États-Unis en 1902 (N° 706650), une formule à deux lentilles en
ménisques très creux, parfaitement symétrique.
http://chestofbooks.com/arts/photography/Practical-Photography-2/
Part-I-Extreme-Wide-Angle-Photography-Part-2.html
Plus récemment, dans les années 1940-1960 ont été développées des
formules grand angulaires de très haute performance entre 90° et 120° de
couverture, comme le Biogon de chez Zeiss (90°), l’Hologon Zeiss (110°, le
premier modèle n’avait que 3 lentilles de forme spéciale) ou les
Super-Angulons (Schneider) et Grandagons (Rodenstock) dont les derniers
modèles couvrent jusqu’à 110-120° avec très peu de distorsion.
|
|
[17] |
Voir cet article de Michel Guigue sur
www.galerie-photo.com
1er janvier en Cambo ! une prise de vue au papier,
www.galerie-photo.com/premier-janvier-en-cambo.html
en particulier cette image d’un Scheimpflug hors norme !
www.galerie-photo.com/images/Sheimp.jpg
|
|
[18] |
Sur la propriété de stationnarité des images
des objets lointains lorsqu’on pivote l’objectif autour du point nodal image
N’, le film ou le détecteur restant fixe par rapport au paysage, on pourra
se référer à cet article sur
www.galerie-photo.com, en particulier la figure 7 :
Un objectif photographique n’est pas une lentille mince ! Première
partie, introduction aux systèmes optiques centrés épais
www.galerie-photo.com/un-objectif-photo.html
|
|
[19] |
Pour une explication détaillée des effets de
profondeur de champ, y compris quelques notions sur l’effet des traitements
numériques renforçateurs de netteté, nous renvoyons le lecteur lisant
l’anglais ou l’allemand à cet article du Dr. Nasse de chez Carl Zeiss. On
lira en particulier en page 23 une analyse de l’effet des traitement
renforçateurs de netteté sur le rendu de la transition net-flou.
H.H. Nasse, Depth of Field and Bokeh, Carl Zeiss Camera Lens News N°
35, mars 2010,
à télécharger sur le site Carl Zeiss division optiques photographiques.
http://www.zeiss.com/cln, archive,
Camera Lens News N°35, Nine rounded iris blades guarantee images with a
harmonic bokeh, read more.
Lien direct :
http://www.zeiss.com/c12567a8003b8b6f/embedtitelintern/
cln_35_bokeh_en/$file/cln35_bokeh_en.pdf
|
|
[20] |
Henri Peyre, Hyperfocale et profondeur de
champ
www.galerie-photo.com/hyperfocale_et_profondeur_de_champ.html
|
|
[21] |
Simon Clément, Calcphot, un logiciel dédié
au calcul de profondeur de champ,
www.galerie-photo.com/profondeur_de_champ_avec_calcphot.html
|
|
[22] |
Henri Peyre, Feuille de calcul de
profondeur de champ
www.galerie-photo.com/profondeur_de_champ_avec_excel.html
|
|
[23] |
Emmanuel Bigler, Profondeur de Champ et
règle de Scheimpflug : une approche simple
www.galerie-photo.com/profondeur-de-champ-et-scheimpflug.html |
-
Emmanuel Bigler 26 octobre 2010
Télécharger
l'article au format pdf.
dernière modification de cet article
: 2010
|