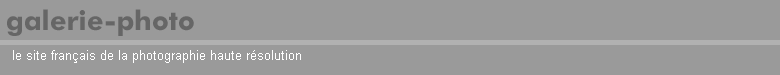|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

l'auteur
Télécharger
cet article
|
Pupilles et raccordement panoramique
Emmanuel Bigler ENSMM, 26 chemin de l’Épitaphe, F-25030 Besançon cedex, Table des matières
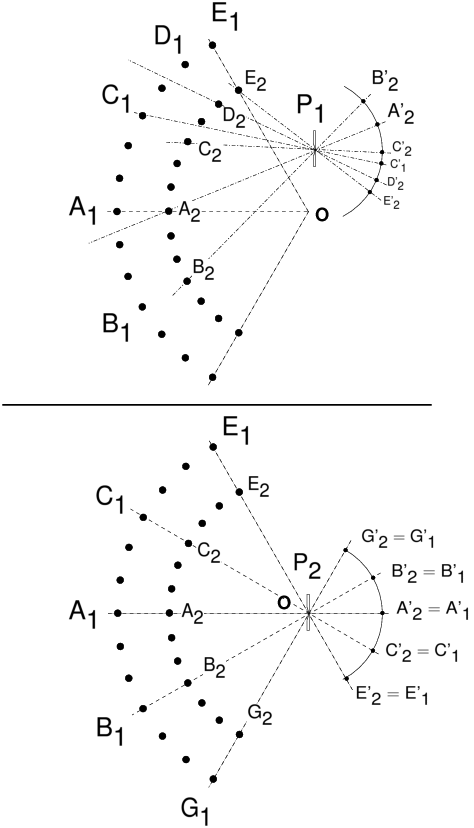
RésuméCet article examine les conditions du meilleur raccordement d’images en photographie panoramique où les prises de vue s’effectuent avec un appareil « ordinaire ». Le rôle de la pupille d’entrée de l’objectif comme point de meilleure rotation minimisant les effets de parallaxe nuisibles au bon raccordement, est analysé en détail. On présente également la question de la reconstruction d’une projection orthoscopique ou cylindrique à partir des projections planes obtenues avec un appareil non spécialisé en photo panoramique. On explique également le fonctionnement des appareils panoramiques à film courbe et objectif tournant. Pour terminer, on présente comment déterminer l’emplacement de la pupille d’entrée d’un objectif. 1 IntroductionLa photographie panoramique par raccordement d’images numériques est une activité qui s’est développée si considérablement au cours de la dernière décennie, que nombre de photographes, amateurs ou professionnels, pratiquent le raccordement panoramique d’images par post-traitement numérique sans se poser plus de questions que M. Jourdain ne s’en posait lorsqu’il écrivait et parlait en prose sans le savoir. Néanmoins les lecteurs exigeants de www.galerie-photo.com et du forum http://www.galerie-photo.info savent que la question du choix du meilleur point de rotation pour que le raccordement s’effectue sans défaut, soulève quelques discussions et fait appel à d’obscures notions d’optique instrumentale. Certes, si vous avez l’occasion de voir l’un de ces « tours d’horizon » de montagne réalisés au siècle dernier par raccordement soigné de tirages sur papier, il est à peu près certain que le photographe de l’époque ne s’est pas préoccupé de savoir autour de quel point il devait faire tourner son appareil. Son souci était plus de savoir comment harmoniser ses temps de pose à la prise de vue et comment équilibrer les densités de ses tirages contigus pour que, mises bord à bord ou massicotées d’un coup, il n’y ait pas de différence de luminosité visible d’une image à l’autre de part et d’autre de la jointure. Aujourd’hui, certains appareils numériques destinés au marché amateur ont une fonction « panoramique automatique » grâce à laquelle vous vous contentez de laisser la machine travailler pour vous pendant que vous balayez l’horizon avec votre appareil en mains, comme l'aurait fait le capitaine d'un bateau faisant son tour d’horizon à la longue vue. Mais avec n’importe quel appareil non panoramique, numérique ou pas, on peut raccorder des images. L’appareil numérique permet d’arriver au résultat bien plus vite qu’au siècle dernier. Avec le raccordement d’images numériques, la pléthore de pixels et la possibilité de regarder à l’écran l’image au pixel près, les défauts de raccordement naguère invisibles, sautent aujourd’hui « numériquement » aux yeux. Il est donc grand temps, alors que la question n’est déjà plus
posée puisque tout le monde se débrouille sans problème, d’analyser
en d���tail la question du meilleur point de rotation dans le
raccordement panoramique d’images effectué avec un appareil
« ordinaire », c’est à dire un appareil qu’on va pointer suivant
différentes directions de l’espace pour enregistrer une succession
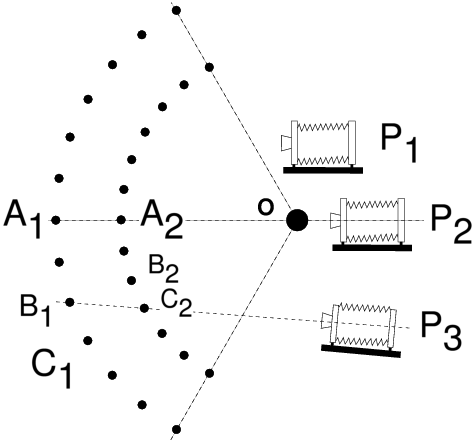
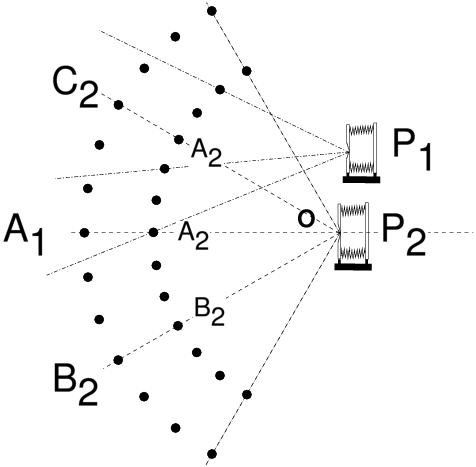
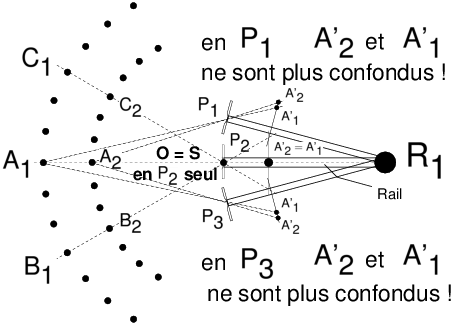
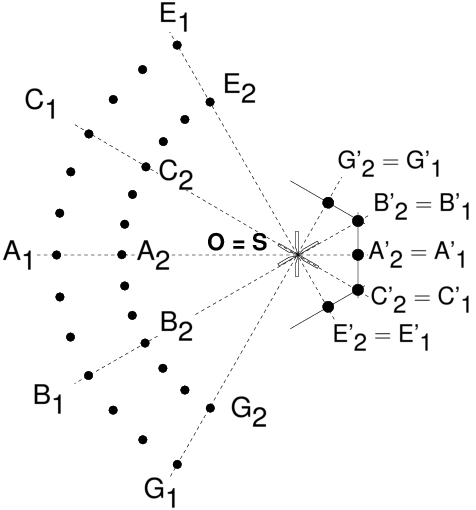
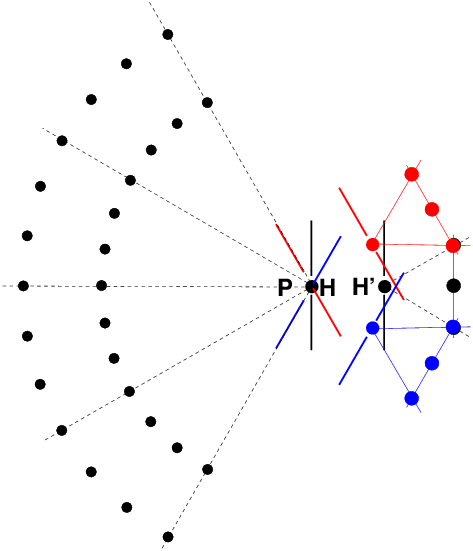
d’images destinées à être raccordées après coup. On va donc examiner pas à pas la question de la projection des images dans cette activité aujourd’hui si répandue qu’est la prise de vue panoramique par raccordement. On commencera par le système le plus simple, le sténopé, dans lequel des tracés géométriques connus depuis la Renaissance permettent de déterminer la manière dont les images se forment dans l’appareil. Suivant le même cheminement que dans l’article traitant du rendu de perspective [1], on passera ensuite à la lentille mince diaphragmée en son centre, puis au système épais symétrique diaphragmé [2], puis de façon plus générale au système dissymétrique avec diaphragme ouvert. Ce cheminement nous amènera à énoncer cette règle simple : pour que le raccordement d’images s’effectue sans défaut, il faut faire tourner l’appareil non pas autour de son écrou de pied, mais autour de la pupille d’entrée de l’objectif. La notion de pupilles dans un objectif photographique a été présentée dans un autre article [3], en plus du rôle déterminant de la pupille d’entrée dans la définition du nombre d’ouverture, cette pupille joue donc un rôle déterminant dans le rendu de perspective et c’est autour du centre de la pupille d’entrée qu’il faut tourner pour effectuer un bon raccordement panoramique. Puis on indiquera plusieurs méthodes simples permettant à tous de déterminer où se situe la pupille d’entrée d’un objectif. Enfin, on expliquera comment les appareils panoramiques spécialisés à film courbe et objectif tournant fonctionnent de façon très différente du raccordement d’images avec un appareil ordinaire. 2 Alignements avec une prise de vue au sténopé2.1 Une colonnade-test imaginairePour commencer et poser le problème du raccordement d’images en photographie panoramique, imaginons que l’on souhaite photographier une double rangée d’arbres plantés suivant deux cercles concentriques, ou bien une double colonnade dans quelque édifice antique imaginaire, dont la vue en plan serait schématisée comme suit (figure 1) : Figure 1: Une scène-test pour poser le problème du raccordement d’images panoramiques Selon l’emplacement de l’appareil, ou point de vue (P1, P2, P3), l’image qui va se projeter sur le dépoli ne permettra pas de voir certaines colonnes cachées par d’autres ; dans le cas particulier du point de vue P2, en visant l’alignement des points A1 et A2, le point A1 sera caché derrière le point A2. Et du point de vue P3, en visant bien, on peut de la même façon cacher le point B1 derrière le point C2. C’est donc une expérience courante en photographie que de voir les changements de point de vue conditionner les alignements ! Qui ne s’est jamais déplacé pour qu’un disgracieux poteau électrique ne soit pas aligné avec tel élément important de la scène photographiée ! 2.2 Une seule image grand-angulaire, au sténopéImaginons que nous souhaitions tirer parti de tout le champ grand-angulaire accessible à notre sténopé sans faire aucun raccordement d’image (figure 2). Avec un sténopé bien conçu, on peut dépasser les 100° d’angle de champ ; peut-être même, étant optimistes, pourrons-nous rêver d’atteindre les 120° que le légendaire Hypergon de chez Görz offrait dès le début du XXe siècle [4]. Prenons comme point de vue l’emplacement P2 sur cette figure 2, et alignons l’appareil à sténopé avec les points A1 et A2. Si, de plus, l’ouverture du sténopé est placée très exactement au centre O, commun aux deux cercles de la double rangée de colonnes, nous enregistrerons en une seule prise : à la fois toute la colonnade ; et vus du point central O, tous les points de la colonnade extérieure tels que A1, B1 seront parfaitement cachés derrière la première rangée A2, B2. Figure 2: Une seule image grand-angulaire, au sténopé, sans raccordement Bien entendu, si le point de vue choisi est tel que P1, nous verrons également l’ensemble de la colonnade, mais les alignements parfaits, propres au point de vue P2 lorsque l’ouverture du sténopé coïncide exactement avec le point O, n’existeront plus dans l’image. Ce simple changement de point vue détruit donc les alignements ; c’est l’effet de parallaxe, le fait que des points qui apparaissent alignés depuis un premier point de vue, ne le sont plus depuis un deuxième point de vue. L’effet de parallaxe est fondamental pour la vision binoculaire ; néanmoins dans toute la suite de cette discussion, nous nous contenterons d’images non stéréoscopiques, et tout au contraire nous chercherons à minimiser les effets de parallaxe induits par un changement de point de vue involontaire lors de l’enregistrement d’images successives par rotation de l’ensemble de l’appareil. 2.3 Le sténopé permet, à volonté, le choix du type de projectionEn renonçant à la netteté, l’appareil à sténopé nous offre en échange la liberté totale de la façon dont l’image se projette sur le film. Plus besoin de faire la mise au point sur une distance donnée ! Par exemple avec un film plan, on obtiendra une projection orthoscopique de la scène, c’est à dire la projection plane, en tableau, connue par tous les peintres et dessinateurs depuis la Renaissance : c’est celle de presque tous les appareils photographiques, à l’exception des appareils panoramiques à objectif tournant et film courbé, un type d’appareil qui sera examiné au paragraphe 6. Figure 3: Projection grand-angulaire orthoscopique avec un appareil à sténopé Figure 4: Projection grand-angulaire cylindrique avec un appareil à sténopé 2.4 Raccordement d’images orthoscopiques avec un sténopéVenons en enfin à l’objet de cet article, qui est de réaliser des images panoramiques avec un appareil « ordinaire », c’est à dire avec un détecteur (film ou silicium) parfaitement plan, en tournant l’appareil dans son ensemble, et en enregistrant en succession, plusieurs images en projection plane qu’il faudra raccorder par la suite. Notre scène-test avec ses colonnades reste inchangée. Imaginons que l’appareil soit fixé sur un rail assez long, l’ensemble (rail plus appareil) constituant un instrument fixe qui tourne d’un bloc. Par notre seule fantaisie, nous décidons arbitrairement de le faire tourner autour d’un point R1 volontairement éloigné du centre S du sténopé. Nous choisissons néanmoins de faire coïncider, dans la position P2, le point S avec le centre de la colonnade O (figure 5). Tournons l’ensemble de l’appareil de façon que celui-ci occupe successivement les trois positions correspondant aux points de vue (P1, P2, P3). Figure 5: Lors de la rotation de l’appareil à sténopé autour d’un point quelconque tel que R1 qui ne coïncide pas avec le centre du sténopé, les points de vue deviennent différents lors de la rotation, par exemple P1, P2 et P3 ; les points-objets A1 et A2, dont les images A’1 et A’2 sont confondues du point de vue P2, n’ont plus leurs images confondues en position P1 ou P3 ; les positions respectives des images A’1 et A’2 s’inversent même lorsqu’on passe de P1 à P3. Les images enregistrées selon ces trois positions ne pourront donc pas se superposer, à cause de l’effet de parallaxe induit par le choix du point de rotation arbitraire R1. Les points-objets A1 et A2, dont les images A’1 et A’2 sont confondues du point de vue P2 aligné avec A1 et A2, n’ont plus leurs images confondues en position P1 ou P3. Les images enregistrées selon ces trois positions ne pourront donc pas se superposer, à cause de l’effet de parallaxe induit par le choix du point de rotation arbitraire R1. À ce stade la discussion, il n’est pas nécessaire d’être un spécialiste du raccordement panoramique pour comprendre que le choix très étrange de tourner autour du point R1 sur la figure 5 conduit à une modification des alignements de l’espace objet d’un point de vue à l����������������autre, et donc conduit à une impossibilité de raccorder ultérieurement les trois images enregistrées depuis les points de vue P1, P2 et P3. La conclusion est donc immédiate : la rotation autour de l’absurde point R1 induit un changement de point de vue et « détruit » les alignements vus, par exemple depuis le point de vue central tel que P2 ! Alors que le choix du point de rotation correct consiste à l’évidence à tourner autour du centre du sténopé (figure 6). Figure 6: Pour que les images se raccordent sans défaut de parallaxe, avec un appareil à sténopé, il suffit de tourner autour du centre du sténopé. Cette règle est très générale, même si on ne photographie pas une double colonnade circulaire depuis son centre ! 3 Raccordement d’images avec une
lentille
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
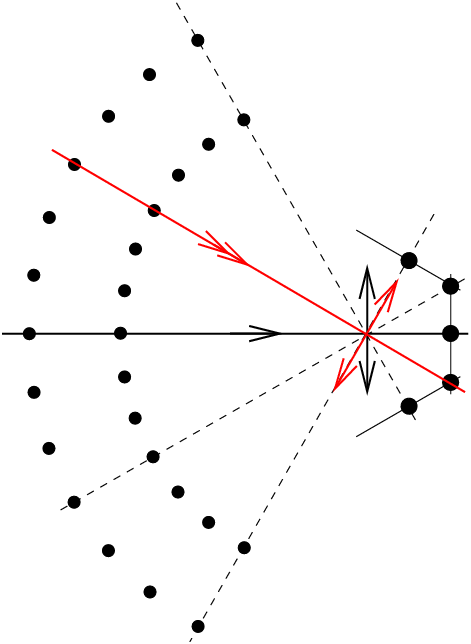
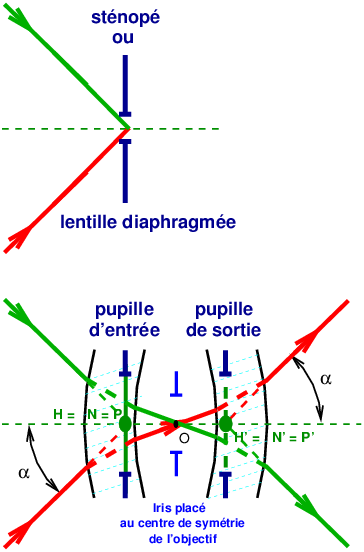
Figure 7: Avec une lentille mince diaphragmée en son centre, ou avec un système parfaitement symétrique diaphragmé, donc en ne prenant en compte que le rayon moyen, passant par le centre de la lentille et qui n’est pas dévié, et en négligeant les défauts de mise au point, le tracé de rayons et le rendu de perspective sont exactement identiques au cas du sténopé. Avec la lentille mince, il faudra donc tourner autour du centre de la lentille.
Avec la lentille mince diaphragmée en son centre, seul passe le rayon moyen qui n’est pas dévié, il n’y a donc aucune différence entre le tracé de la figure pour le sténopé (figure 6) et celle pour la lentille (figure 7).
Avec la lentille mince diaphragmée en son centre, il faudra donc tourner autour du centre de la lentille pour que le raccordement d’images s’effectue sans changement de point de vue, donc sans défauts de parallaxe.
3.2 Raccordement avec un système symétrique diaphragmé
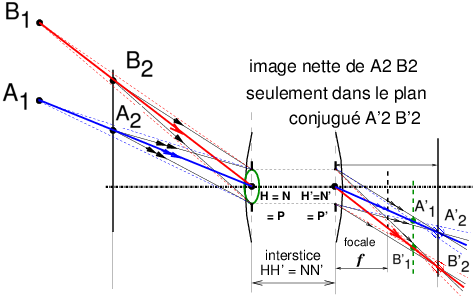
Figure 8: Dans un système épais parfaitement symétrique, les pupilles P et P’ coïncident avec les points principaux H et H’, lesquels sont confondus avec les points nodaux N et N’ pour un système fonctionnant dans l’air. Le point autour duquel il faut tourner le système épais pour être dans les mêmes conditions de minimisation des effets de parallaxe que sur la figure 6 avec le sténopé, est donc l’endroit où convergeraient les rayons alignés avec les colonnes, s’ils n’entraient pas dans le système, c’est à dire au niveau de l’image du diaphragme vu de l’avant, appelée pupille d’entrée.
Le tracé de rayons pour la lentille diaphragmée en son centre est donc exactement le même que pour le sténopé ; mais personne n’utilise de lentille mince pour faire de belles images et encore moins pour faire du raccordement panoramique ! Or il se trouve que le tracé pour un système épais parfaitement symétrique (avec diaphragme placé au centre de symétrie) est exactement le même, du côté de l’objet, que pour la lentille. Du côté de l’image, la seule différence entre la lentille mince et le système symétrique épais est le recul du tracé, d’une distance HH’ ou interstice, écart entre les plans principaux H et H’. On se reportera à cet article [1] pour les détails sur ces questions de rendu de perspective comparatifs entre un sténopé, une lentille et un système épais symétrique.
Figure 9: Construction analogue à celle de la figure 6, mais pour un système centré parfaitement symétrique, dont le diaphragme est placé au centre de symétrie, et dont, en conséquence, les pupilles sont aux plans principaux. Avec le système épais, pour tourner de façon à ne pas modifier les alignements vus du côté de l’objet, il faudra donc tourner autour du point principal objet H qui correspond également à la position de la pupille d’entrée P dans ce cas particulier d’un système symétrique.
3.3 Effet de défocalisation dans un système symétrique
Nous avons donc presque terminé l’analyse, du moins pour un système symétrique. Avant de passer au cas général du système dissymétrique, on peut d’abord se poser la question de l’influence du défaut de mise au point sur le raccordement d’images. En effet, les défauts de parallaxe n’existent que si l’on cherche à photographier des objets étalés en profondeur, dans un volume. Si on ne photographiait que des objets plats, il n’y aurait pas d’effet de parallaxe.
L’absence d’effets de parallaxe, c’est également la situation en raccordement panoramique pour paysage lointain [5], lorsqu’il n’y a pas de premier plan ; dans ce cas, avec un objet à l’infini et pas de premier plan, on peut tourner l’appareil autour de n’importe quel point !
On voit donc que c’est l’étagement en profondeur qui crée les problèmes de raccordement si on ne tourne pas l’appareil autour de sa pupille d’entrée, mais n’anticipons pas encore sur le cas général qui sera étudié un peu plus loin (paragraphe 4).
Une particularité des images défocalisées qu’on forme derrière une optique symétrique, est que ces images sont affectées d’un facteur de grandissement analogue à ce qu’on peut tirer du modèle du sténopé (voir figure 10). Mais lors de l’enregistrement de l’image, les images floues se forment de telle façon que les points alignés de l’espace objet, comme A1 et A2, qui sont alignés avec la pupille d’entrée P = H = N, apparaissent confondus dans l’image résultant de l’empilement de toutes les images défocalisées. Afin que d’une image à l’autre, en tournant l’appareil, ces alignements de l’espace objet soient rendus de la même façon quel que soit l’angle de rotation de l’appareil, il suffit donc de tourner autour de la pupille d’entrée.
Figure 10: Dans un système symétrique, la construction des images défocalisées est exactement identique à la construction des images dans un appareil à sténopé ; et les images floues se forment de telle façon que les points alignés de l’espace objet, comme A1 et A2 qui sont alignés avec la pupille d’entrée P, apparaissent confondus dans l’image résultant de l’empilement de toutes les images défocalisées le long de la ligne P’A’1.
4 Raccordement panoramique avec une optique dissymétrique : pupille d’entrée !
4.1 Tracé de rayons expliquant le rôle de la pupille d’entrée dans les effets de parallaxe
Examinons maintenant le cas général, optique dissymétrique et diaphragme ouvert. Le tracé se complique nettement, mais la conclusion concernant le rôle de la pupille d’entrée pour le raccordement panoramique ne change pas (figure 11).
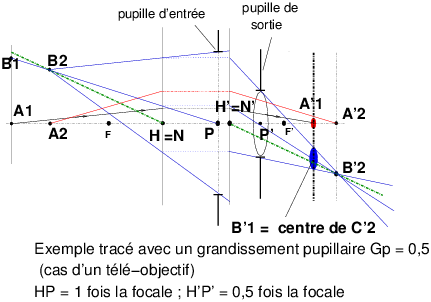
Le système est dissymétrique avec ses pupilles P et P’ situées en dehors des plans principaux H et H’. Sur la figure 11, on a tracé l’exemple d’un télé-objectif avec un grandissement pupillaire Gp = 0,5. Nous renvoyons le lecteur à l’article sur les pupilles pour la définition du grandissement pupillaire [3]. Dans le cas d’une optique dissymétrique avec grandissement pupillaire de 0,5, la pupille d’entrée est située à une fois la focale derrière le point principal objet H, et la pupille de sortie est située à une demi fois la focale derrière le point principal image H’.
Examinons le tracé de rayons de la figure 11.
B’1 est l��������������������������image nette de B1. B'2 est l’image nette de B2, elle se forme derrière B’1.
C’2 est la pseudo-image défocalisée de B2, c’est un cercle, projection de la pupille de sortie à travers le plan A’1–C’2, le centre de cette projection conique est B’2.
P’, C’2 et B’2 sont alignés d’après les lois de la projection conique.
Donc, la condition pour que B1 et B2 semblent « alignés » sur la photo est que B’1 soit confondu avec C’2.
La conséquence en est que B1, B2 et P sont alignés si et seulement si P’, B’1 = le centre de la tache C’2 et B’2 sont alignés.
Figure 11: Dans un système dissymétrique, la construction des images défocalisées devient différente de celle du sténopé ; ce qui ne change pas par rapport a cas du système symétrique, c’est le fait que les images floues sont formées par projection de la pupille de sortie le long du rayon moyen, c’est à dire le rayon passant par le centre des pupilles P et P’. En revanche les deux rayons moyens B2P et P’B’2 ne forment pas le même angle par rapport à l’axe optique A2A’2, car les pupilles ne sont plus placées aux points principaux (ou points nodaux).
On voit ici que les formules de conjugaison n’interviennent
qu’indirectement. Pour les pseudo-images défocalisées, c’est la
position des pupilles et la position des images nettes qui
définissent leur position et leur grandeur.
Le problème de parallaxe est
directement lié au fait de détecter dans l’image un empilement entre
des images nettes et des pseudo-images défocalisées ; ce problème
est donc conditionné par la position de la pupille de sortie vis à
vis des images enregistrées, et la position relative de la pupille
d’entrée vis à vis de la scène à photographier.
4.2 Reformulation du problème à partir des images
Il semble naturel pour résoudre le problème posé initialement, de partir de l’espace objet, de lancer des rayons, et de voir comment ils se propagent jusqu’au plan du détecteur. C’est la démarche suivie jusqu’à ce point de la discussion. Mais comme souvent dans les problèmes d’optique instrumentale, il est plus fructueux de considérer les images en traçant le moins de rayons possibles.
Oublions notre colonnade-test, ne cherchons même pas à savoir si notre système optique est simple ou complexe, symétrique ou dissymétrique, oublions ses foyers et ses plans principaux, et considérons un point du détecteur, tel que B’1 sur la figure 11. En B’1 se forme l’image nette du point source B1 si nous avons fait notre mise au point correctement sur B1.
La question à se poser est finalement très simple :
Quels sont les points de l’espace objet dont l’image défocalisée sera centrée en B’1 ?
Les images défocalisées (par exemple celles qui se focaliseraient
parfaitement en B’2)
se projettent sur B’1
en suivant la ligne P’B’1
qui joint le centre de la pupille de sortie au point
B’1. Les
taches de défocalisation ont la forme d’un petit cercle
(si l’iris est circulaire, mais
cela peut être un pentagone) dont le diamètre est d’autant
plus grand que la défocalisation augmente.
Mais le point-clé de l’argumentaire est que
ce cercle est centré sur la ligne
joignant le centre de la pupille de sortie
P’ à l’image nette
B’1 (figure11).
Donc dans l’espace objet, ce rayon moyen provient du rayon passant par les points conjugués de P’ et B’1, soit la ligne B1P ; et donc tous les points objet hors du plan de netteté, dont l’image se projette centrée sur B’1, sont situés nécessairement sur cette ligne B1P. Si on bouge la position de la pupille d’entrée P pendant la rotation, les différentes images défocalisées qui « s’empilent » sur le point B’1 de notre détecteur correspondent à des alignements différents pour les différents angles de rotation, et les alignements correspondant au point de vue P2 de la figure 5 seront perdus. Il ne faut pas que le centre de la pupille d’entrée P bouge lors de la rotation de l’appareil, donc il faut tourner autour de la pupille d’entrée. Les foyers, les plans principaux, les points nodaux et la focale de l’objectif n’interviennent pas directement dans cette affaire liée à l’empilement d’images défocalisés.
La règle générale, pour une optique épaisse dissymétrique, afin d’éviter les défauts de parallaxe dans le raccordement d’images avec un appareil ordinaire, est donc qu’il faut tourner l’ensemble de l’appareil autour de la pupille d’entrée de l’objectif.
5 Mais où se trouve la pupille d’entrée de mon objectif ?
5.1 En lisant la fiche technique du constructeur
Certains constructeurs comme Zeiss et Schneider-Kreuznach publient les spécifications détaillées de leurs objectifs, avec la position des pupilles mesurées par rapport aux montures et aux sommets de la première et de la dernière lentille.
On peut lire par exemple sur la fiche technique Zeiss du planar 3,5 de 100 mm les données suivantes, en anglais [6] :
|
Position of entrance pupil: |
32.9 mm |
behind the first lens vertex |
|
Diameter of entrance pupil: |
28.7 mm |
|
|
Position of exit pupil: |
42.6 mm |
in front of the last lens vertex |
|
Diameter of exit pupil: |
33.4 mm |
|
|
Position of principal plane H: |
42.2 mm |
behind the first lens vertex |
|
Position of principal plane H’: |
27.1 mm |
in front of the last lens vertex |
|
Distance between first and |
||
|
last lens vertex: |
57.2 mm |
Ce qui se traduit simplement :
|
Position de la pupille d’entrée : |
32,9 mm |
derrière le sommet de la première lentille |
|
Diamètre de la pupille d’entrée : |
28,7 mm |
|
|
Position de la pupille de sortie : |
42,6 mm |
devant le sommet de la dernière lentille |
|
Diamètre de la pupille de sortie : |
33,4 mm |
|
|
Position du plan principal H: |
42,2 mm |
derrière le sommet de la première lentille |
|
Position du plan principal H’: |
27,1 mm |
devant le sommet de la dernière lentille |
|
Distance entre les sommets de la |
||
|
première et de la dernière lentille : |
57,2 mm |
De ces données on tire d’abord le grandissement pupillaire =
(diamètre pupille de sortie) / (diamètre de pupille d’entrée) = 33,4
/ 28,7 = 1,16.
Le planar 3,5 de 100 mm n’est pas tout à fait symétrique, mais il
est très proche d’une formule symétrique (grandissement pupillaire
proche de 1).
Les autres données nous permettent de placer les éléments cardinaux sur le schéma suivant (figure 12) :
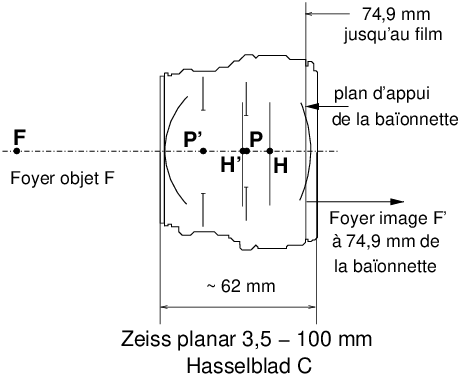
Figure 12: Position des éléments cardinaux : foyer, plans principaux et pupilles, dans l’objectif Zeiss Planar 3,5 - 100 mm Hasselblad C (d’après la fiche technique du constructeur [6])
On constate que les plans principaux du planar 3,5 de 100 mm sont « croisés » (plan principal objet en arrière du plan principal image), ce qui arrive régulièrement dans les objectifs photographiques ; les pupilles sont également croisées (pupille de sortie en avant de la pupille d’entrée). La pupille d’entrée P, située à 32,9 mm derrière le sommet de la première lentille, tombe à peu près au milieu de l’objectif. C’est à dire très en avant du filetage qui se situe sous le sabot de fixation du boîtier.
5.2 Par le calcul à partir du brevet décrivant l’optique
Si on dispose du brevet décrivant l’optique, donc la liste des rayons de courbure, des espacements entre dioptres et des caractéristiques des verres employés, un logiciel de simulation des systèmes optiques n’aura aucune difficulté à déterminer la position et le diamètre des pupilles. C’est la fonctionnalité de détermination des éléments paraxiaux de l’optique qui est utilisée, l’une des plus simples pour les logiciels de calcul optique. On trouvera dans l’annexe 9 un exemple de résultat de simulation avec le logiciel Oslo-EduMD pour l’objectif Heliar (5 lentilles en 3 groupes), d’après le brevet original de 1902 de Hans Harting chez Voigtländer.
5.3 Optique quasi-symétrique, comme la plupart des optiques de chambre
Dans la plupart des optiques de chambre, à l’exception des télé-objectifs, l’écart entre plans principaux est faible, le grandissement pupillaire est proche de l’unité, la pupille d’entrée se trouve donc proche du point H, qui se trouve en général à quelques millimètres du plan d’appui en face avant de la planchette, là où l’obturateur s’appuie. Par exemple pour la série des Apo Ronars Rodenstock, des formules presque parfaitement symétriques, l’écart entre plans principaux n’excède pas quelques pourcents de la distance focale, et la pupille d’entrée est toujours située très proche du centre de symétrie de l’objectif.
5.4 Optique dissymétrique, télé-objectif ou grand-angulaire « rétrofocus »
Il n’est pas possible de donner des règles générales concernant la position des plans principaux et des pupilles pour les optiques dissymétriques. Les optiques grand angulaires de type rétrofocus ont un grandissement pupillaire plus grand que l’unité, la pupille d’entrée se trouve le plus souvent vers l’avant de l’objectif. Pour un télé-objectif, c’est l’inverse, le grandissement pupillaire est plus petit que l’unité, et il n’est pas impossible que la pupille d’entrée d’un télé-objectif tombe au niveau du plan focal, c’est à dire, paradoxalement tout à fait à la « sortie » de l’appareil !
Pour un zoom trans-standard, en général on a un comportement de rétrofocus en position grand angle (pupille d’entrée vers l’avant) et de télé-objectif en longue focale (pupille d’entrée très enfoncée vers l’arrière), la pupille d’entrée se déplace fortement d’avant et arrière lorsqu’on passe des courtes aux longues focales. On peut le voir très facilement en observant l’image du diaphragme vu par devant, lorsqu’on tourne la bague des focales du zoom.
5.5 Déterminer expérimentalement la position d’une pupille d’entrée
Il n’est pas difficile d’estimer la position de la pupille d’entrée d’un objectif soi-même sans besoin d’aucun équipement professionnel. Il suffit de se souvenir que la pupille d’entrée est visible lorsqu’on regarde l’objectif depuis l’avant, c’est l’image du diaphragme donnée par les groupes de lentille antérieurs, c’est à dire les groupes de lentilles placés en avant de l’iris.
5.5.1 Optiques dont la pupille d’entrée est accessible directement
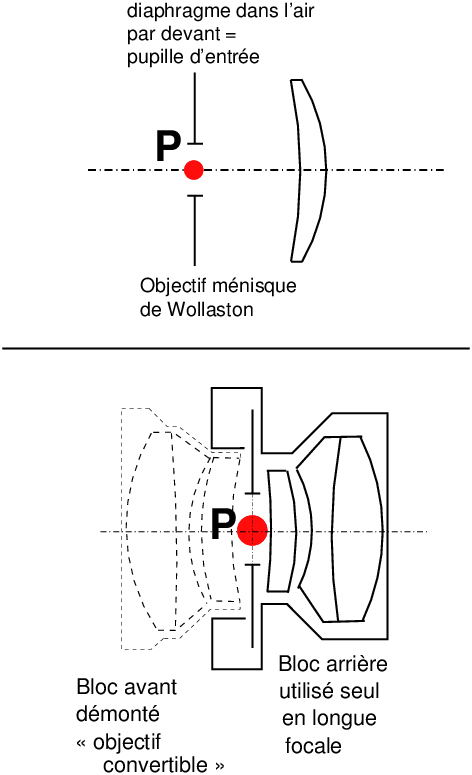
Certaines optiques très particulières permettent néanmoins d’accéder directement à la pupille d’entrée : c’est le cas du ménisque de Wollaston [8], qui est formé d’une lentille simple diaphragmée par devant, de l’Imagon de chez Rodenstock, un doublet dont le diaphragme est également placé devant les verres ; ou encore une optique de chambre « convertible », dans laquelle on a dévissé le groupe avant pour ne se servir que du groupe arrière, placé derrière l’obturateur et le diaphragme (figure 13).
Figure 13: Lorsque le diaphragme est dans l’air, devant les verres, la pupille d’entrée de l’objectif est simplement ce diaphragme
Dans ces cas très particuliers, la pupille d’entrée du système est tout simplement l’iris qui est dans l’air. En revanche dans ces systèmes, la pupille de sortie est bien entendu l’image de l’iris vu de l’arrière à travers les lentilles, et non pas l’iris lui même.
5.5.2 Pointé de la pupille d’entrée par tracé sur un bristol
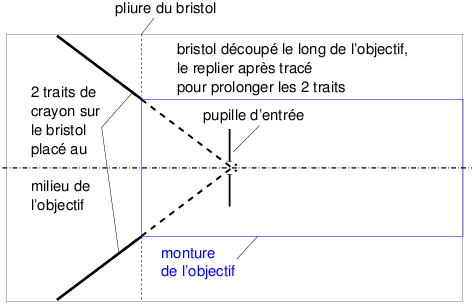
Avec une optique un peu moins particulière que les précédentes, munies d’un groupe optique devant l’iris, il suffit de fermer le diaphragme pour bien voir le centre de la pupille d’entrée et de viser ce point en faisant un tracé à la règle et au crayon sur une feuille de papier (figure 14).
Figure 14: Détermination de la position de pupille d’entrée par un tracé sur un bristol
Fermez le diaphragme au maximum et procédez comme suit.
Vous montez votre objectif sur une chambre, sur son boîtier à monture à baïonnette, ou sur n’importe quel support permettant de mettre l’axe optique horizontal dans le plan de la table. Vous vous munissez d’un bristol suffisamment grand pour que vous puissiez dessiner dessus à la fois un élément de référence en entrée, par exemple le bord de la monture de filtre, et le point où se situe la pupille d’entrée. Vous découpez le bristol d’un volet rectangulaire dont la largeur est celle de la monture, vous le repliez par en-dessous le temps du pointé.
À l’oeil, vous visez les deux alignements du centre de la pupille avec les bords de monture de la lentille frontale, vous tracez deux droites à la règle sur le bristol, en avant de l’objectif, selon ces alignements. Vous dépliez le volet et vous prolongez les deux droites : là où elles se croisent se trouve le centre de votre pupille d’entrée.
5.5.3 Photographie de la pupille d’entrée avec un autre appareil, en macro
Une autre méthode consiste à utiliser l’équivalent d’un viseur optique à distance frontale fixe. Prenez un appareil reflex quel qu’il soit, avec un bon verre de visée avec télémètre à champ coupé, muni d’une optique macro ou d’un soufflet pour pouvoir faire la netteté sur la pupille d’entrée. Comme vous visez très probablement à pleine ouverture, vous aurez le moins de profondeur de champ possible, ce qui vous donne un bon pointé longitudinal très précis.
Faites la netteté sur le bord du diaphragme, vu à travers le groupe optique avant, l’iris n’a plus besoin d’être fermé au maximum. Ne touchez pas aux réglages de l’appareil servant de viseur, reculez l’appareil-viseur, son soufflet et son optique, en bloc, jusqu’à voir net l’avant de la monture d’objectif dont on veut pointer la pupille d’entrée : c’est fait ! Du déplacement de votre « viseur à frontale fixe » vous en déduisez la distance entre le bord de monture et la pupille d’entrée.
La méthode du pointé avec un autre appareil utilisé à une distance de mise au point et un grandissement fixes (par exemple 1:1) permet, en plus, de déterminer le grandissement pupillaire en pointant d’un côté puis de l’autre de l’objectif. Et en pointant une règle graduée toujours sans bouger les réglages de l’appareil, si l’appareil est un appareil numérique, en comptant les pixels et par comparaison, on a accès à une mesure très précise des diamètres de pupilles ... sauf quand la pupille a une forme de pentagone, auquel cas on mesure autre chose qu’un diamètre de cercle ;-) )
5.5.4 Autres méthodes, à lire sur le web
On peut également déterminer la position du point de rotation qui minimise les effets de parallaxe. Cette méthode simple et efficace est expliquée en détail sur la page web de M. Hamblenne, « La Grille » [9].
Voir également les pages web d’Arnaud Frich où sont expliquées en détail et en images différentes méthodes de détermination de la position de la pupille d’entrée [10].
6 Appareil panoramique à film courbe et objectif tournant
Dans l’état actuel de la technique, les appareils numériques à capteur silicium étant tous munis d’un capteur parfaitement plan, M. de La Palice nous aurait fait remarquer que ce genre d’appareil à film courbe n’existe qu’avec du film. Ce en quoi M. de La Palice n’aurait pas complètement tort, mais il ne faut pas oublier qu’on peut également se servir d’un papier photo comme surface sensible.
Le principe de la projection cylindrique dans ce type d’appareil consiste à faire tourner l’objectif devant un film plaqué sur un cylindre, la rotation s’effectuant en synchronisme avec une fente verticale fine centrée sur l’axe optique tournant (figure 15). De ce fait, seule une mince bande d’image est enregistrée à chaque instant, la totalité de l’image sur support courbe est donc formée par le raccordement de fines bandes contiguës. La netteté est assurée, pour des objets lointains, en plaçant le film dans le plan focal « tournant » et en limitant latéralement, par une fente fine, la portion de cylindre exposée à chaque étape pour éviter la défocalisation due à la projection sur une surface cylindrique.
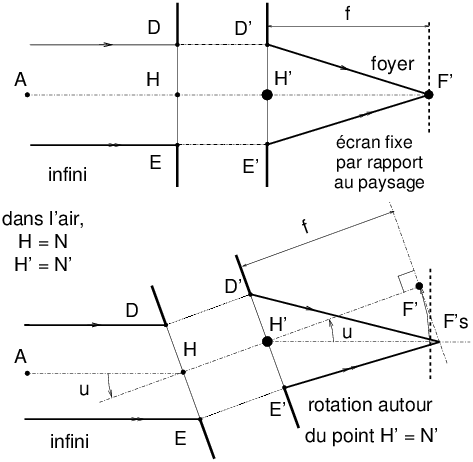
Figure 15: Principe de l’appareil panoramique à film courbe et objectif tournant. Sur cette figure, on a simplifié l’objectif pour le représenter par une simple lentille mince convergente, dont les plans principaux ou nodaux sont confondus avec le centre de la lentille. Avec une optique épaisse, la stationnarité de l’image d’un objet lointain lors de la rotation de l’objectif impose de tourner l’optique autour de son point nodal image N’.
Dans ce genre d’appareil, il est indispensable de faire tourner
l���objectif autour de son point
principal image H’,
ou encore point nodal image
N’, ou encore
point nodal d’émergence
N’. Pour une
optique utilisée dans l’air, les points nodaux et les points
principaux sont confondus ;
H = N et
H’ = N’. La rotation
autour de H’ = N’ est
requise pour que l’image reste nette au cours de la rotation de
l’objectif, la raison en est rappelée sur la figure
suivante (figure 16).
Lorsqu’on tourne un objectif devant une scène fixe, avec un film
courbé mais fixe par rapport à la scène, l’image se déplace
toujours pendant la
rotation, sauf si on tourne l’objectif autour du point nodal
d’émergence N’.
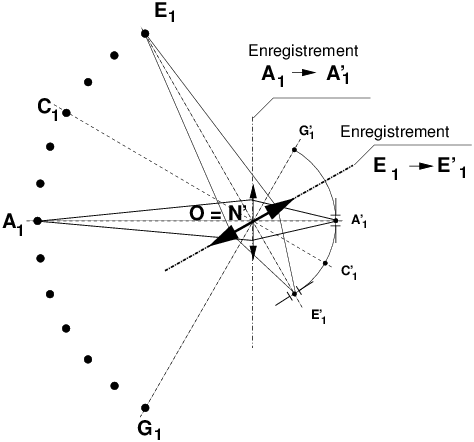
Figure 16: Lors de la rotation de l’objectif, pour que l’image d’une scène lointaine reste fixe, donc nette, sur un film qui ne bouge pas par rapport à la scène photographié, il est nécessaire de tourner l’objectif autour de son point principal image H’, ou point nodal image N’ ; l’objet étant lointain, le film devra donc être placé au foyer de l’objectif pour que la mise au point soit bonne, la distance H’F’ étant par définition égale à la focale de l’objectif. Notons que cette propriété utilise la propriété fondamentale des points nodaux N et N’, deux points conjugués l’un de l’autre à travers le système, et pour lesquels l’angle d’inclinaison u est conservé entre l’entrée en N et la sortie en N’. À aucun moment les propriétés des pupilles ne sont impliquées dans le raisonnement, et donc ce problème de stationnarité des images avec un objectif tournant est totalement décorrélé de la question des effets de parallaxe lors du raccordement d’images avec un appareil ordinaire.
On forme sur un écran fixe par rapport au paysage l’image d’une scène très éloignée de façon qu’on puisse la considérer comme à l’infini. Un professionnel de la métrologie optique utiliserait un collimateur, l’amateur se contentera comme objet de l’immeuble d’en face ou d’un clocher.
Il faut être capable de faire pivoter l’objectif autour de n’importe quel point de l’axe optique ; ceci suppose de disposer d’une glissière, ou d’une chambre monorail réduite à son seul corps avant. L’image doit se former sur un écran ou un dépoli désolidarisé de l’objectif, on va chercher à ce qu’elle reste fixe par rapport à l’objet.
On fait pivoter l’objectif autour de l’axe dans un sens puis dans l’autre ; on constate que dans la plupart des cas l’image se déplace dans un sens puis dans l’autre, sauf dans une position bien particulière de l’axe de rotation qui correspond au point nodal image N′, identique dans l’air au point principal image H’.
En réalité si on y regarde de près (figure 16) on voit que la propriété des points nodaux de conserver l’angle de sortie u′ égal à u maintient le rayon H’F’s parallèle au rayon moyen AH en entrée. Si l’optique n’a pas de courbure de champ, le point F’s après rotation est situé un tout petit peu en arrière de l’écran. Pour expliquer cela il faut se représenter le tracé classique en appliquant les règles mais en tenant compte du fait que l’axe optique et le foyer F’ ont tourné ; c’est par rapport à cette nouvelle position qu’il faut faire le tracé. Un faisceau de rayons parallèles à AH se focalise en un point du plan focal F’s, mais le plan ayant tourné autour de H’, le point de focalisation F’s n’est plus tout à fait situé sur l’écran, mais un peu en arrière : l’image devient floue.
Dans cette expérience du « tourniquet », même si on tourne correctement autour du point H’ = N’, même si aux grands angles de rotation l’image reste quasi-stationnaire, elle se défocalise un peu. Mais l’important est que le rayon H’F’s reste parallèle à la direction des rayons incidents. Cette propriété de stationnarité s’étend de façon approchée aux autres point de l’image, qui eux proviennent de la focalisation de rayons non parallèles à AH, ce qui rend l’ensemble de l’image stationnaire.
L’image de l’objet à l’infini se formant dans le plan focal passant par F’, la détermination du point nodal image N’ = H’ nous donne –en remettant l’axe du système optique perpendiculaire à l’écran– la focale f du système épais, égale à H’F’.
Cette propriété de stationnarité de l’image pour un objet à l’infini est à la base du réglage optique des appareils panoramiques à fente mobile et tambour rotatif, pour lesquels l’image doit rester stationnaire par rapport au film pendant que l’objectif tourne.
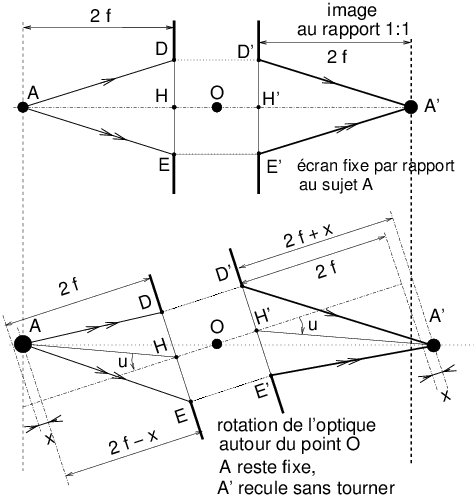
Notons également que la rotation autour du point nodal image n’assure la stationnarité de l’image que pour des objets lointains, avec formation des bandes d’images au foyer de l’objectif. Pour d’autres configurations (objet -> image) différentes de la conjugaison (infini -> foyer), ce sera un autre point de rotation qui assurera la stationnarité. Par exemple, pour une conjugaison de type (2f -> 2f) au rapport 1:1 avec une optique épaisse parfaitement symétrique, il faudrait tourner autour du centre de symétrie de l’objectif (figure 17).
Figure 17: Lors de la rotation d’un objectif,
avec un objet fixe
A
et un détecteur fixe, en position « 2f -> 2f »,
au grandissement 1:1, avec une optique
parfaitement symétrique, c’est autour du centre
de symétrie de l’objectif
O
qu’il faut tourner pour assurer la stationnarité de l’image
On voit donc que le point nodal image n’a absolument rien à voir avec les questions de parallaxe en raccordement d’images avec un appareil ordinaire !
7 Conclusion
-
Les effets de parallaxe intempestifs en raccordement panoramique d’images par rotation de l’ensemble de l’appareil ne sont à prendre en compte que lorsque l’image contient des premiers plans rapprochés ; en panorama de paysage lointain sans premier plan, ces effets sont minimes et peuvent être ignorés ;
-
Plus important est le choix du type de projection en vue du rendu final de l’image, qui la plupart du temps est exposée à plat : projection orthoscopique grand-angulaire, projections cylindrique ou sphérique ; le choix de ces projections conditionne le rendu des lignes droites et l’esthétique générale de l’image (en particulier les déformations des objets en bord de champ) ;
-
Pour minimiser les effets de parallaxe intempestifs en raccordement panoramique avec un appareil « ordinaire » il suffit de tourner l’appareil autour de la pupille d’entrée de l’objectif ; il est facile de déterminer la position de cette pupille d’entrée sans instrumentation spéciale ;
-
Les appareils panoramiques à film courbe et objectif tournant réalisent directement une projection cylindrique ; le fait que l’objectif doive tourner autour de son point principal (ou nodal) image est totalement décorrélé des effets de parallaxe précédents.
Remerciements
Cet article n’existerait pas sans la discussion initiale que l’auteur a eue avec Yves Colombe, échange dont on trouvera la trace dans les archives du forum de http://www.galerie-photo.info. La discussion portait sur ce fameux point de rotation qui minimise les effets de parallaxe en raccordement panoramique, l’archive est en référence ici [12].
L’auteur remercie vivement M. Richard Knoppow du groupe de discussion Rollei [13] pour avoir bien voulu mettre à disposition son fichier de définition de l’Heliar pour la simulation avec le logiciel Oslo-EduMD.
8 Annexe : post-traitement des perspectives
8.1 Raccordement et présentation « à l’ancienne »
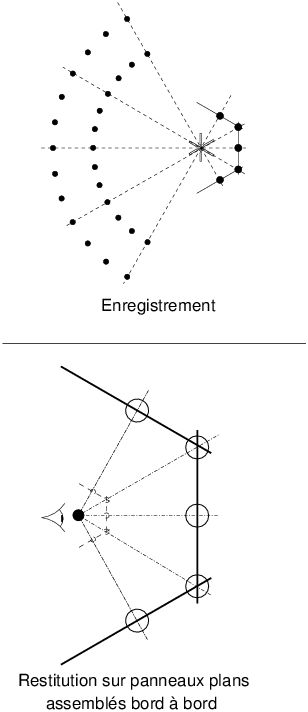
Avant l’ère de l’image numérique & ses post-traitements obligés, il n’y avait en principe qu’une seule façon de présenter des images obtenues par raccordement, de façon que celui qui regarde les tirages voie exactement ce qu’on peut regarder sur le terrain (figure 18).
Figure 18: Sans post-traitement numérique, seule une présentation des tirages sur un assemblage polygonal (ou plutôt : prismatique) de panneaux plans mis bord à bord peut redonner un rendu de perspective conforme à la réalité, mais uniquement pour un observateur placé en un seul point bien choisi.
Bien que géométriquement correcte, cette façon de procéder est purement théorique et n’a jamais dû être beaucoup utilisée pour des expositions par le passé, ne serait-ce que parce que le rendu de perspective correct n’est visible que depuis un seul point « central » ; et que de toutes façons, il est très difficile de cacher les raccords entre panneaux. Donc on se contentait de montrer l’assemblage à plat, tirages mis bord bord, ce qui correspond géométriquement à déplier les panneaux latéraux pour les aligner avec le panneau central. Ce faisant, on tombe sur un autre problème, c’est que les grandes lignes droites qui traversent l’ensemble du panorama dans la scène photographiée, apparaissent alors comme des lignes brisées. En d’autres termes, chaque vue qui compose le panorama est une vue orthoscopique, donc l’image d’une droite se projette comme une droite, mais l’assemblage panoramique vu en plan représente ces lignes comme une succession de morceaux de droite faisant un angle entre elles.
Dans l’un de ses fameux ouvrages didactiques du siècle dernier [11], René Bouillot n’avait pas de mots assez durs pour fustiger cette pratique du raccordement panoramique « à l’ancienne », indigne, à l’époque, d’un photographe professionnel sérieux. Les développements de la prise de vue numérique et des post-traitements associés répondent aujourd’hui entièrement à ces objections légitimes, en permettant des raccordements d’images panoramiques parfaitement maîtrisés en tous points :
-
automatisation possible de la prise de vue par un mécanisme robotisé gérant les pointés successifs et les déclenchements de l’appareil sans aucune intervention du photographe ;
-
corrections adaptatives des différences d’exposition d'une vue à l’autre,
-
raccords géométriques parfaitement invisibles d’une vue à l’autre,
-
choix de la projection finale entre orthoscopique grand-angulaire, cylindrique ou sphérique.
8.2 Correction géométrique des projections par post-traitement numérique
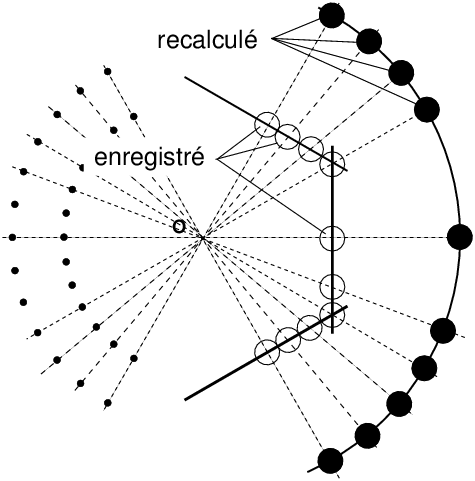
Avec le raccordement d’images numériques, non seulement les miracles logiciels raccordent les morceaux comme par magie, mais en plus, on a le choix de reconstruire, à partir des morceaux de projections orthoscopiques planes, d’autres types de projections en recalculant complètement les images à partir des données enregistrées lors d’une succession de projections planes.
8.2.1 Reconstruction d’une projection orthoscopique ultra grand-angulaire
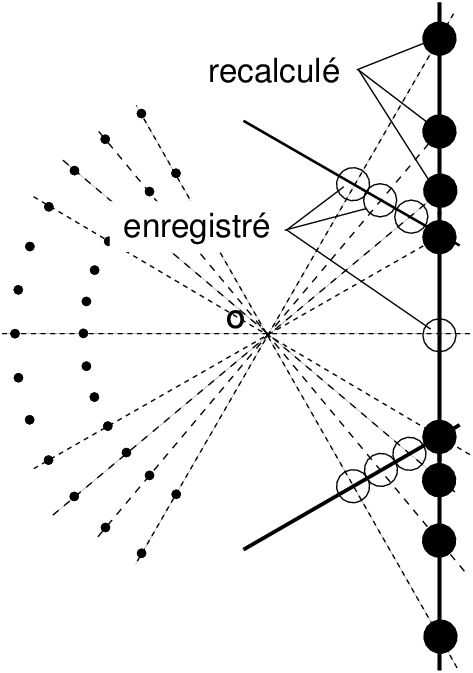
La correction géométrique la plus simple consiste à reconstituer l’équivalent d’une projection orthoscopique grand-angulaire, c’est à dire celle qu’on obtiendrait au sténopé, ou bien avec un objectif ultra grand-angulaire à faible distorsion, à partir des projections élémentaires (figure 19).
Figure 19: Un post-traitement num����������rique permet de choisir un assemblage avec reconstitution d’une projection orthoscopique ultra grand-angulaire
8.2.2 Reconstruction d’une projection cylindrique
L’inconvénient de la projection orthoscopique grand-angulaire, au-delà de 90°, est qu’elle engendre des « déformations » en bord de champ. A ce sujet, voir cet autre article sur les rendus de perspective [1], en particulier les figures 13 et 14.
Pour un panorama, la perspective cylindrique présente l’avantage de ne pas rendre les bords de champ différemment du centre. En contrepartie, les grandes lignes droites sont représentées par des courbes, à l’exception de toutes les verticales et de la ligne d’horizon vers laquelle pointe l’axe optique.
Figure 20: Post-traitement numérique pour la reconstitution d’une projection cylindrique
Le post-traitement numérique consiste donc à recalculer à partir des projections planes, ce qu’aurait été une projection cylindrique, c’est à dire une projection très proche de ce qui serait obtenu avec un appareil à optique tournante et film plaqué sur un cylindre ; puis à raccorder les morceaux et à présenter l’image finale à plat. On peut bien entendu rouler à nouveau le tirage et le présenter sur un cylindre, mais on retombe sur l’inconvénient précédent, un seul point de vue pour l’observation, le centre du cylindre, donnera un rendu « naturel » ; donc autant en rester à un panorama cylindrique, observé à plat après avoir été « déroulé ».
8.2.3 Reconstruction d’une projection « sphérique »
Le raccordement d’images numériques ne se limite pas à un seul angle de rotation panoramique, on peut également raccorder des bandes d’images obtenues en combinant un mouvement de panorama et un mouvement de plongée / contre-plongée. Certains logiciels spécialisés proposent alors une reconstitution de « projection sphérique » ; les morceaux de sphère sur lesquels on aurait pu inscrire les projections avec un sténopé et une surface sensible acceptant de se plaquer sur une sphère (donc probablement une couche à badigeonner soi-même sur une sphère, car le film ne peut se plaquer que sur une surface développable comme un cylindre ou un cône) sont donc recalculés à partir des projections planes élémentaires. Il faut ensuite faire choix d’une « mise à plat » de cette sphère : les différentes projections utilisées pour la représentations du globe terrestre dans les atlas suggèrent qu’un très grand nombre de projections sphère->plan sont possibles, on s’éloigne alors de la belle simplicité de la projection cylindrique.
9 Annexe : détermination des éléments cardinaux d’une optique avec Oslo-EduMD
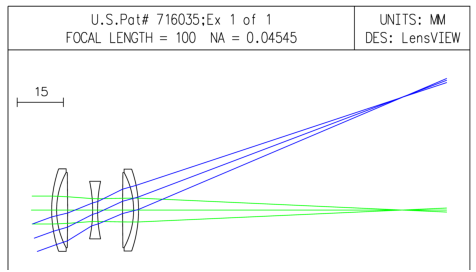
Voici par exemple ce que donne le logiciel Oslo-EduMD [7] pour l’Heliar de Hans Harting, breveté en 1902.
Figure 21: Simulation d’une optique classique, ici : l’Heliar de Hans Harting (1902), avec le logiciel Oslo-EduMD ; à partir des caractéristiques des verres et les dimensions des lentilles, la détermination de la position et du diamètre des pupilles par le calcul est une fonctionnalité élémentaire incluse dans l’analyse des propriétés paraxiales de l’objectif.
Les données du brevet doivent tout d’abord être saisies sous forme d’un tableau utilisable par le logiciel :
*LENS DATA Heliar 1902 U.S.Pat# 716035 SRF RADIUS THICKNESS APERTURE RADIUS GLASS SPE NOTE OBJ -- 1.0000e+20 3.6397e+19 AIR 1 40.952608 1.598150 13.391628 LV1 2 25.730217 3.595838 12.232451 LV2 3 -583.123363 8.090636 12.232451 AIR 4 -44.708247 1.598150 9.365994 LV4 5 44.708247 1.997688 9.221742 AIR AST -- 6.092948 3.728073 AS AIR 7 583.123363 3.595838 12.232195 LV7 8 -25.730217 1.598150 12.232195 LV8 9 -40.952608 85.419837 13.308923 AIR IMS -- -- 36.397023 S
Ensuite on lance l’analyse paraxiale, qui permet de déterminer les éléments cardinaux dans l’approximation de Gauss ; les données ci-dessus sont dimensionnées pour un Heliar de 100 mm de focale, la simulation est faite avec un diamètre de pupille d’entrée correspondant à l’ouverture f/11, donc un diamètre de 100/11 = 9 mm (rayon de 4,5 mm).
*PARAXIAL SETUP OF LENS APERTURE Entrance beam radius: 4.545455 Image axial ray slope: -0.045455 Object num. aperture: 4.5455e-20 F-number: 11.000000 Image num. aperture: 0.045455 Working F-number: * 11.000000 FIELD Field angle: * 20.000000 Object height: -3.6397e+19 Gaussian image height: 36.397023 Chief ray ims height: 36.397023 CONJUGATES Object distance: 1.0000e+20 Srf 1 to prin. pt. 1: 14.580163 Gaussian image dist.: 85.419836 Srf 9 to prin. pt. 2: -14.580163 Overall lens length: 28.167399 Total track length: 1.0000e+20 Paraxial magnification: -1.0000e-18 Srf 9 to image srf: 85.419837 OTHER DATA Entrance pupil radius: 4.545455 Srf 1 to entrance pup.: 18.351919 Exit pupil radius: 4.380242 Srf 9 to exit pupil: -10.945498 Lagrange invariant: -1.654410 Petzval radius: -241.417787 Effective focal length: 99.999999
On trouve ainsi la position des plans principaux, ainsi que la position et le diamètre des pupilles :
distance entre le premier (1) et le dernier dioptre (9) : 28,17 mm iris placé à 2 mm derrière la surface N°5, 16,9 mm derrière le dioptre N°1 plan principal objet H à 14,58 mm derrière le sommet du premier dioptre (1) plan principal image H' à 14,58 mm en avant du sommet du dernier dioptre (9) Pupille d'entrée à 18,35 mm derrière le premier dioptre (1) - diam. 9 mm Pupille de sortie à 10,95 mm en avant du dernier dioptre (9) - diam. 8,8 mm
L’Heliar de 1902 est une formule parfaitement symétrique, dans la simulation précédente, la seule petite dissymétrie provient du placement du diaphragme qui est un peu derrière la lentille divergente centrale.
Notes et Références
|
|
« Angles de champ, focales,
projections et rendu de perspective », E. Bigler,
|
|
|
« Un objectif photographique
n’est pas une lentille mince ! Introduction aux systèmes
optiques centrés épais », E. Bigler et Y. Colombe,
|
| [3] |
« Lumière, diaphragme et
pupilles », E. Bigler,
|
| [4] |
Frank Mechelhoff, « Early Super
Wide Angle Lenses »,
|
| [5] |
Lors de la prise de vue panoramique d’un paysage de montagne, les effets de parallaxe existent bien évidemment. Par exemple tout randonneur parcourant les crêtes du Jura cherchera à identifier les sommets des Alpes ; depuis le milieu de l’arc jurassien, il est fréquent de pouvoir apercevoir le sommet du Cervin qui est en arrière-plan des préalpes bernoises et vaudoises. À un kilomètre près, soit un déplacement d’un quart d’heure de marche, il est fréquent que le Cervin apparaisse ou disparaisse, caché par d’autres sommets. Mais si vous placez votre appareil photo en un lieu où le Cervin est visible, pour que l’effet de parallaxe du raccordement panoramique autour d’un point de rotation mal choisi fasse disparaître ce pic emblématique, il faudrait monter l’appareil au bout d’un rail de plusieurs centaines de mètres de long.
|
| [6] |
Fiche technique en anglais pour
le planar 3,5 100 mm version C en monture Hasselblad V
|
| [7] |
Le logiciel de simulation optique
Oslo-EduMD est distribué par la société Lambda
Research Corporation, on peut le télécharger librement ici :
|
| [8] |
http://en.wikipedia.org/wiki/
|
| [9] |
Pages web d'Alain Hamblenne,
méthode de la grille pour déterminer le point de rotation qui
minimise les effets de parallaxe.
|
| [10] |
Site web d’Arnaud Frich sur la
photo panoramique, voir la section relative à la détermination
de la pupille d’entrée d’un objectif.
|
| [11] |
René Bouillot « La Pratique du
Moyen Format », éditions VM, ISBN 2-86258-129-11, (Paris, 1993)
|
| [12] |
Discussion avec Yves Colombe sur
le raccordement panoramique et la pupille d’entr��������������e (avril
2002) :
http://www.galerie-photo.org/a-f-498.html |
| [13] |
Archives du groupe de
discussion Rollei RUG-List |
Télécharger
cet article
au format pdf
Dernière modification 2014
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||