Les sténopés n'ont pas de cercle d'image,
seulement des cercles de confusion.
La théorie
par Paul Kopff
Dans l'article jumeau :
“Les
sténopés n'ont pas de cercle d'image, seulement des cercles de
confusion. La pratique”
sont présentés deux outils de simulation écrits
en javaScript, qui montrent sous la forme de courbes l'effet des
paramètres d'un appareil à sténopé (focale, diamètre et épaisseur du
sténopé, etc.) sur le vignettage et la résolution des images. Car
deux types d'appareils sont envisagés :
Les appareils classiques
: des boites parallélépipédiques, où le sténopé est au centre d'une
face et où la pellicule couvre l'intérieur de la face opposée.
Les appareils anamorphiques
: les plus courants sont des boites cylindriques, où le sténopé est
au centre du couvercle et où la pellicule couvre l'intérieur de
toute la face latérale cylindrique. Ce deuxième type d'appareils a
déjà été décrit en détail. Ils font des
photographies panoramiques sur des angles pouvant approcher les 360°
suivant des perspectives qui paraissent très déformées.
Pour ceux qui veulent comprendre la théorie
derrière les programmes qui tracent de si jolies courbes voici en
détail mes arguments pour justifier ces modèles et quelques formules,
dont on m'a dit qu'elles étaient trop compliquées pour la plupart,
mais que je crois du niveau de la terminale S (sauf si ce niveau a
baissé beaucoup plus que je ne le pensais...)
1/ Les sténopés n'ont pas de cercle d'image...
Les fabricants d'optiques pour appareils
photographiques garantissent (dépendant de la formule optique
adoptée) un cône à l'intérieur duquel on peut considérer que les
aberrations des images sont suffisamment bien corrigées et la
transmission de la lumière suffisamment uniforme. Dans le plan de
l'image, ce cône dessine un cercle appelé cercle d'image. On
constate qu'à l'intérieur de ce cercle, on observe une image assez
uniformément claire et précise mais qu'à l'extérieur, elle
s'assombrit rapidement (et perd parfois aussi en netteté).
Les appareils photographiques à sténopé n'ont pas
d'optique ; au lieu de cela, l'image est dessinée par la lumière
passant par un trou minuscule appelé “sténopé” (du grec “stenos”
petit et “ops” oeil) percé dans une membrane opaque encore plus fine
(valeurs typiques – diamètre du sténopé : 0,3mm – épaisseur de la
membrane : 0,01mm).
Contrairement aux objectifs, les sténopés n'ont
pas de cercle d'image nettement défini : l'image s'assombrit très
progressivement en s'éloignant de l'axe de prise de vue (plus
exactement, de l'axe du sténopé, perpendiculaire à la membrane dans
laquelle il est percé).
Ayant principalement construit des appareils à
sténopé “anamorphiques”, qui recueillent des images très en dehors
de l'axe du sténopé, je me suis intéressé à comparer la façon dont
ces images s'assombrissent par rapport aux appareils à sténopé
“classiques” dans lesquels l'image est recueillie dans l'axe du
sténopé sur une surface sensible perpendiculaire à cet axe...
suivant la conception classique de la “camera obscura”.
J'ai donc élaboré deux modèles mathématiques de
cet assombrissement progressif, le premier pour les appareils à
sténopé classiques et le second pour les appareils dits “anamorphiques”.
1a/ Modèle du
vignettage des appareils classiques
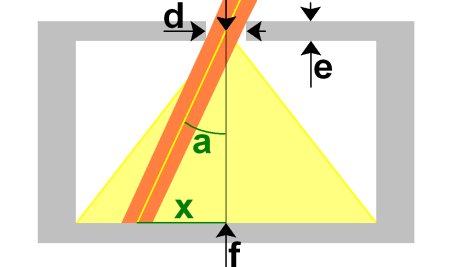
Ce premier modèle considère une membrane
d'épaisseur e percée d'un petit trou circulaire de diamètre d, et à
la distance f de ce sténopé suivant son axe, une surface sensible
plane parallèle à la membrane (et donc perpendiculaire à l'axe du
sténopé).
L'angle d'incidence de la lumière provenant d'un
point lumineux à l'infini (très loin par rapport au diamètre du
sténopé) est repéré par rapport à l'axe, mais on considèrera aussi
(et de préférence) la distance x de l'image de ce point au
“centre” de la surface sensible (qui est l'intersection de l'axe du
sténopé avec ce plan).
Comme la source ponctuelle est très loin, mais
que le sténopé n'a pas un diamètre nul, ce n'est pas un rayon
lumineux idéal qui le traverse, mais un très étroit faisceau
lumineux qu'on pourra considérer cylindrique. Quand il ne traverse
pas le sténopé suivant son axe mais suivant un angle d'incidence a,
ce faisceau cylindrique n'est pas circulaire mais pincé suivant une
ellipse et donc de surface réduite d'un premier facteur cos(a).
Mais ce n'est pas la seule cause
d'assombrissement de l'image.
Pour poursuivre rigoureusement la démonstration,
il faut considérer que le point lumineux fait partie d'une petite
source étendue (par exemple le Soleil ou la Lune, qui vus de la
Terre ont un diamètre apparent d'environ ½ degré). A la distance f
du sténopé leur image a une certaine luminosité, mais si cette
source n'est pas dans l'axe, elle est projetée à une distance
supérieure, elle est donc plus grande et moins lumineuse encore :
d'un deuxième facteur d'assombrissement cos²(a).
Enfin, il faut tenir compte du fait que le plan
de la surface sensible n'est pas perpendiculaire au faisceau de
lumière qui y arrive ce qui ajoute un dernier facteur
d'assombrissement cos(a).
En combinant ces trois facteurs, on estime qu'en
s'éloignant de l'axe du sténopé l'image s'assombrit d'un facteur
cos(a) à la puissance 4, ce qui conduit par exemple à la perte de
2ev entre le centre de l'image et le cercle des rayons incidents à
45° (ce résultat est bien connu).
1b/ Modèle du
vignettage des appareils anamorphiques
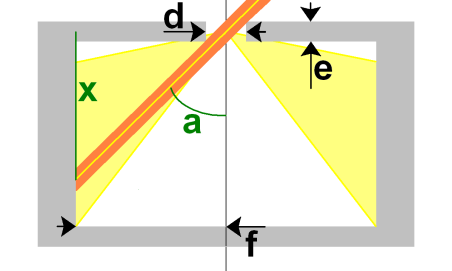
Ce type d'appareils forment la surface sensible
suivant un cylindre dont l'axe est confondu avec celui du sténopé.
Ce ne sont donc que des rayons lumineux inclinés qui
l'impressionnent.
Pour les appareils à sténopé classiques, c'était
facile, on pouvait exprimer l'assombrissement par rapport au centre
de la surface sensible (dans l'axe du sténopé). Eh bien, faisons par
la pensée de même pour les appareils anamorphiques (étant entendu
que dans l'axe du sténopé, il n'y a en réalité pas de surface
sensible).
On peut reprendre les mêmes notations que pour le
modèle des appareils classiques : d est le diamètre du sténopé, e
l'épaisseur de la membrane, f pour cette fois sera le rayon du
cylindre formant la surface sensible, et aussi la distance du
sténopé au point à la distance f sur son axe, qui fait office de
référence ; a étant l'angle d'incidence des rayons lumineux formant
une image en un point de la surface sensible distant de x du plan de
la membrane où est percé le sténopé.
Reprenant les trois facteurs d'assombrissement,
on voit qu'il n'y a rien de changé pour le premier : du fait du
pincement en ellipse des faisceaux lumineux il vaut toujours cos(a).
Mais le deuxième, causé par l'allongement de la distance du sténopé
à la surface sensible vaut sin²(a). Et comme la surface sensible
n'est plus parallèle au plan de la membrane, mais à l'axe du sténopé,
le troisième facteur vaut sin(a).
Et en combinant ces trois facteurs, on estime
qu'à l'incidence a par rapport à l'axe du sténopé, l'image
s'assombrit d'un facteur sin(a) à la puissance 3 que multiplie cos(a).
Il est clair que la fonction cos(a) à la
puissance 4, de même que la fonction cos(a) prend une valeur
maximale pour a = 0, c'est à dire dans l'axe du sténopé. Mais il
n'en est pas de même pour la fonction sin³(a)cos(a) dont il faut
étudier la dérivée pour conclure : on montre que le maximum de cette
fonction vaut 0,325 pour un angle d'incidence de 60°.
En prenant comme dans le cas du modèle des
appareils classiques le log base 2 de cette valeur, on constate que
ce maximum est déjà assombri de 1,623ev par rapport au point de
référence hypothétique dans l'axe du sténopé.
Autre fait remarquable, à une incidence de 45° on
trouve 2ev d'assombrissement comme dans le cas du modèle des
appareils à sténopé classiques.
Il est par conséquent évident que le “diaphragme”
apparent du sténopé d'un appareil anamorphique est nettement plus
fermé que celui d'un appareil classique : d'un peu plus de 1,5
“diaphs” !!! mais que les variations de l'assombrissement – et donc
le vignettage – semblent être plus contenues.
1c/ Prise en
compte de l'épaisseur de la membrane
Mais encore : ces premières considérations n'ont
pas pris en compte l'influence de l'épaisseur de la membrane quand
elle n'est pas négligeable devant le diamètre du sténopé. J'ai bien
mis ce paramètre e sur la figure mais je ne l'ai pas utilisé !? Son
influence est d'accroître le pincement des faisceaux lumineux
inclinés jusqu'à les éteindre complètement aux incidences les plus
rasantes. Le facteur correcteur est assez difficile à établir,
faites donc confiance au savant fou !
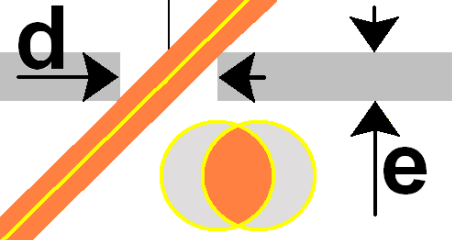
Tout se passe comme si le contour du trou sur la
face supérieure de la membrane et celui sur la face inférieure
étaient décalés l'un par rapport à l'autre, d'autant plus que
l'angle d'incidence a est plus grand, donc la lumière plus rasante.
On trouve donc que la superficie du trou au lieu de valoir π d²/4
vaut :
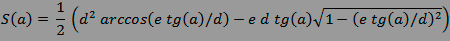
Bouffre !
On vérifie que pour a = 0 ou pour e = 0 cette
formule donne π d²/4 , c'est rassurant, ouf ! A noter aussi que ce
résultat n'est positif et donc valable qu'à la condition que tg(a) <
d/e : car un résultat négatif signifierait que la lumière est trop
rasante et qu'elle est complètement obturée par l'épaisseur de la
membrane.
1d/ Paramétrage en
fonction de la position d'un point de l'image
Il reste une petite chose à faire pour rendre ces
formules vraiment sympathiques : y remplacer toutes les références à
l'angle d'incidence a par des références à la position x d'un point
de l'image sur la surface sensible.
C'est facile, il suffit de remarquer que tg(a)
peut être remplacé par x/f dans le cas des appareils classiques et
par f/x dans le cas des appareils anamorphiques, et aussi que :
cos²(a)
peut être remplacé dans le cas des appareils classiques par :
1 / ( 1 + tg²(a) )
sin²(a)
peut être remplacé dans le cas des appareils anamorphique par :
1 / ( 1 + 1/tg²(a) )
ce qui revient très sympathiquement à la même
fonction de x/f :
1 / ( 1 + (x/f)² )
et enfin que sin(a) cos(a) vaut : 1 / ( tg(a) +
1/tg(a) ) = 1 / ( x/f + f/x )
Sans se tromper dans des calculs certes assez
laborieux on trouve alors finalement les formules de
l'assombrissement en fonction de x,
dans le cas des appareils à sténopé classiques :
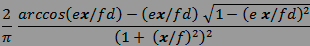
et dans le cas des appareils à sténopé anamorphiques :
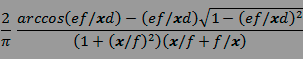
formules dont “il suffit” de “prendre le logarithme base deux” pour
obtenir des EV (les diaphs (!) de différence entre l'éclairement du
centre de l'image et l'éclairement à distance x).
Les sténopés n'ont donc pas de cercle d'image...
2/ ... seulement des cercles de confusion.
La grande angoisse des sténopistes est de trouver
le diamètre “optimal” de leur sténopé.
D'après la loi fondamentale de l'optique
géométrique, suivant laquelle la lumière se propage dans un milieu
transparent homogène suivant des droites (eh oui !), chaque faisceau
lumineux provenant d'une source ponctuelle et traversant le sténopé
dessine sur la surface sensible une petite tache dont les dimensions
et la forme dépendent de la section du sténopé, de l'angle
d'incidence de la lumière qui le traverse et de la distance à
laquelle et de l'angle suivant lequel elle tombe sur la surface
sensible.
2a/ “Cercle” de
confusion géométrique dans le cas d'un appareil à sténopé classique
Soit un appareil à sténopé classique, où la
membrane dans laquelle le sténopé est percé et la surface sensible
sont parallèles ; si le sténopé est un petit trou circulaire de
diamètre d et si l'épaisseur e de la membrane est négligeable
relativement à d, chaque petite tache image d'une source ponctuelle
est un petit cercle de diamètre d. Et l'image d'une source étendue a
une taille proportionnelle à la distance f entre le sténopé et la
surface sensible, dans laquelle les petits cercles “se confusionnent”
plus ou moins ; et c'est pour cela qu'on les appelle des “cercles de
confusion”.
On obtient donc une image plus ou moins grande
suivant f mais toujours avec la même résolution dépendant de d . On
a donc apparemment intérêt à diminuer le diamètre d et à augmenter
la distance f pour obtenir des images plus détaillées.
Plus précisément, comme dans les modèles de
vignettage, il faut tenir compte de l'angle d'incidence et de
l'épaisseur de la membrane, mais cette fois non plus globalement –
pour la superficie apparente du sténopé – mais séparément – pour ses
deux dimensions apparentes : “radiale” (suivant la direction allant
du centre de l'image sur l'axe du sténopé vers un point à distance x
– ou sous une incidence a) et “tangentielle” (suivant la direction
perpendiculaire, c'est à dire en fait suivant la tangente au cercle
de rayon x). Car les “taches” de confusion ne sont plus des cercles
mais adoptent la forme pincée montrée sur la troisième figure
ci-dessus.
Le savant fou trouve comme dimension radiale de
la tache de confusion géométrique :
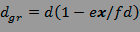
et comme dimension tangentielle :
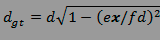
mais bien sûr comme on l'a déjà mentionné, à la
condition que x/f < d/e , sinon il y a extinction complète des
faisceaux lumineux.
Ces formules semblent prouver que les dimensions
des taches de confusion ont une légère tendance à diminuer quand
l'incidence augmente. Hélas, ce n'est pas si simple.
2b/ “Cercle” de confusion diffractive dans
le cas d'un appareil à sténopé classique
En effet, quand elle passe à travers des trous
très petits, la lumière se rappelle son caractère ondulatoire et
nous fait la méchante farce de s'étaler par diffraction.
Le savant fou vous fait grâce des calculs très
compliqués pour vous donner la formule simple qui est utilisée dans
tous les calculateurs du diamètre optimal des sténopés.
Pour un sténopé de diamètre d, à distance f de la
surface sensible, l'étalement d'un rayon lumineux par diffraction a
un diamètre dd , inversement proportionnel à d et aussi
fonction de la longueur d'onde w de la lumière :
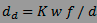
K est une “constante” dont on dispute la valeur
entre 2 et 4 (ce qui n'a qu'une importance relative puisqu'entre le
rouge et le violet, w prend également des valeurs variant du simple
au double).
Les calculateurs de diamètre optimal des sténopés
ne font rien de plus que d'égaler d et dd, ce qui revient
à poser que pour le diamètre optimal d'un sténopé, la confusion
géométrique doit être du même ordre de grandeur que la diffraction.
Ils trouvent ainsi que le diamètre optimal do vaut :
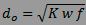
Mais naturellement, tout cela n'est valable qu'à
incidence nulle, dans l'axe du sténopé. Car pour toute autre
incidence, il faut tenir compte de la forme apparente du sténopé vu
depuis le point de l'image à la distance x de son axe. Le savant fou
ne l'est pas au point de se farcir des calculs rigoureux pour
trouver les formes exactes des taches de diffraction, il réutilise
de façon heuristique les résultats déjà établis sur les dimensions
apparentes radiale et tangentielle et l'ovalisation ; ce modèle
donne donc seulement une estimation approchée mais suffisante
de la dimension radiale de la tache de confusion
diffractive :
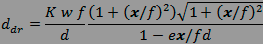
et de sa dimension tangentielle :
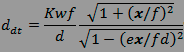
En tant que telles, ces formules peuvent tout de
même encore sembler barbares, mais les petits outils JavaScript que
je présente dans l'article
jumeau permettent de comparer l'importance relative des quatres
dimensions de confusion en jouant sur les paramètres f , e , w et d
grâce à des règlettes.
On peut donc optimiser beaucoup mieux le
dimensionnement des sténopés qu'avec les outils classiques (qui
n'implémentent que la formule simple pour do donnée plus
haut – valable seulement dans l'axe du sténopé), surtout dans le cas
de réalisations “extrémistes” comme les appareils super-grand-angulaires,
panoramiques ou anamorphiques.
Justement, revenons-y aux appareils
anamorphiques :
Tout d'abord, il est à noter que les directions
suivant lesquelles on repère les deux dimensions des taches de
confusion (géométriques et diffractives) ne sont pas les mêmes que
dans le cas des appreils classiques :
–
le “radial” des appareils classiques est
en fait dirigé suivant la “verticale” du panorama anamorphique,
c'est à dire suivant la plus petite dimension du cadre,
–
le “tangentiel” quant à lui est dirigé
suivant l' “horizontale” du panorama anamorphique, c'est à dire
suivant la plus grande dimension du cadre.
Cela dit, les formules se ressemblent beaucoup,
sauf qu'il faut tenir compte du fait que le plan du sténopé est non
plus parallèle au plan de l'image, mais perpendiculaire au plan
tangent au cylindre qui porte l'image en tout point de celle-ci :
ce qui échange en particulier x et f dans les expressions on l'on
trouve aussi e et d (et seulement dans celles-là).
Rappelons enfin que x est ici la distance du
point considéré de l'image au plan de la membrane dans laquelle
est percé le sténopé. Donnons plus laconiquement les résultats :
2c/ “Cercle” de
confusion géométrique dans le cas d'un appareil à sténopé
anamorphique
Le savant fou trouve comme dimension verticale de
la tache de confusion géométrique :
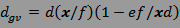
et comme dimension horizontale :
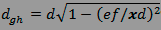
2d/ “Cercle” de
confusion diffractive dans le cas d'un appareil à sténopé
anamorphique
Et voici aussi l'estimation approchée mais
suffisante
de la dimension verticale de la tache de
confusion diffractive :
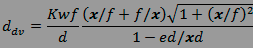
et de sa dimension horizontale :
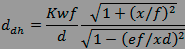
à noter bien sûr comme auparavant, tout cela
n'est valable qu'à la condition que x/f > e/d , sinon il y a
extinction complète des faisceaux lumineux.
Et voilà, c'est tout ! Ce n'était pas plus
compliqué que cela. En fait, c'est même une approche très simplifiée
– surtout dans l'analyse du phénomène de diffraction ; car il
fallait trouver des formules utilisables avec ces outils de
programmation relativement rudimentaires et peu performants que sont
les interpréteurs javaScript.
3/ Place aux travaux pratiques et aux
“outils” !
Ces deux outils présentent exactement le même
aspect : ils montrent des courbes fonctions de x suivant un axe
horizontal. Au dessus de cet axe il y a quatre courbes de couleur
différentes montrant comment varient en fonction de x les dimensions
radiales (resp. verticales) et tangentielles (resp. horizontales)
des taches de confusion géométriques et diffractives. En dessous de
l'axe, une courbe unique montre en fonction de x comment l'image
s'assombrit. Les quatres courbes des “confusions” sont repérés
suivant un axe gradué en mm (millimètres) et la courbe de
“vignettage” l'est en EV (exposure value, ou – en français – IL :
indice de lumination).
3a/ Outil de
simulation des appareils à sténopé classiques
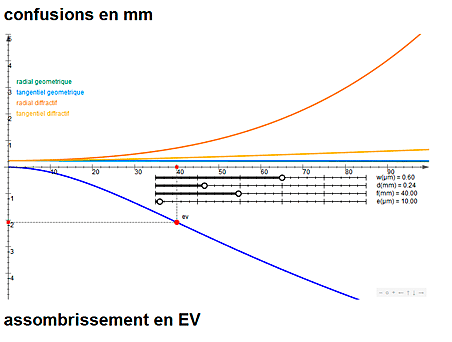
Pour cet outil, x représente sur la surface du
film la distance (en mm) d'un point dans n'importe quelle direction
par rapport au “centre” de l'image, qui est le point du film à la
perpendiculaire du sténopé. Et la “focale” f (en mm) est la
distance entre ce point “centre” de l'image et le sténopé.
3b/ Outil de
simulation des appareils à sténopé anamorphiques
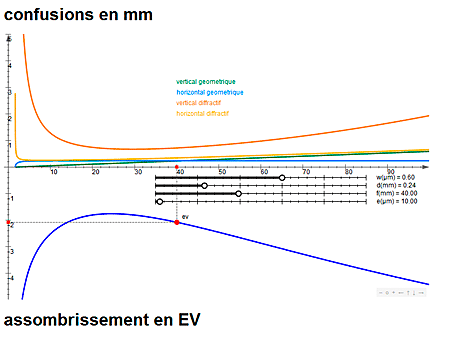
Dans ces appareils, le film est déroulé à
l'intérieur d'un cylindre de rayon f (en mm) et le sténopé est percé
au centre de son “couvercle”. Pour ce deuxième outil de simulation,
x (en mm) est la distance “normale” d'un point de la pellicule au
couvercle.
Les valeurs initiales des deux outils/modèles
considèrent une “focale” f de 40mm et un diamètre du sténopé
“optimisé” suivant la formule “agréée”, qu'on peut utiliser pour
commencer avec confiance.
Des explications plus détaillées (plus
pédagogiques ?) quant à l'intérêt et au mode d'emploi de ces deux
outils de simulation – ainsi que deux études de cas se trouvent dans
l'article jumeau :
“Les
sténopés n'ont pas de cercle d'image, seulement des cercles de
confusion.La pratique” |

